1/n 与 n-1 位循环节

142857

近期刷到了一个视频，说 142857 这串数字如何的神秘，与古埃及有如何如何的关系。由于它分别乘以 1~6 都还是这串数，所以叫什么走马灯数，如何如何。抛开神秘学话题，这就是简单的 1/7 循环节：

不过『走马灯数』这个概念还是有点意思的。它最显著的特征是循环节长度 = n-1，同时附带的性质是当乘以 $1, 2, 3, \cdots, n-1$ 时，循环节顺序和长度不变，只是起始位置换了一下。因此写了段程序简单搜索一下还有没有其它的 n 也有这个特征。

const loop = (n) => {
    let a = 1
    let pool = new Set()

    while (true) {
        a = a % n * 10
        if (a === 0) { return "" }   // 除尽没有循环节
        let digi = (a / n) | 0
        let b = a + digi
        if (pool.has(b)) {          // 当当前位的值和当前余数都出现过时，新的循环开始了
            let loop = [...pool]
            let index = loop.findIndex(i => i === b)
            let str = loop.slice(index).map(e => e % 10).join('')
            return str
        } else {
            pool.add(b)
        }
    }
}

let start = 7
while (start < 1000) {
    let str = loop(start)
    if (str.length == start - 1) { console.log(start, str) }
    start++
}

结果出乎意料地多：

1/n	循环节
1/7	142857
1/17	0588235294117647
1/19	052631578947368421
1/23	0434782608695652173913
1/29	0344827586206896551724137931
1/47	0212765957446808510638297872340425531914893617
1/59	0169491525423728813559322033898305084745762711864406779661
1/61	016393442622950819672131147540983606557377049180327868852459
1/97	010309278350515463917525773195876288659793814432989690721649484536082474226804123711340206185567
1/109	009174311926605504587155963302752293577981651376146788990825688073394495412844036697247706422018348623853211
1/113	0088495575221238938053097345132743362831858407079646017699115044247787610619469026548672566371681415929203539823
1/131	0076335877862595419847328244274809160305343511450381679389312977099236641221374045801526717557251908396946564885496183206106870229
1/149	0067114093959731543624161073825503355704697986577181208053691275167785234899328859060402684563758389261744966442953020134228187919463087248322147651
1/167	0059880239520958083832335329341317365269461077844311377245508982035928143712574850299401197604790419161676646706586826347305389221556886227544910179640718562874251497
1/179	0055865921787709497206703910614525139664804469273743016759776536312849162011173184357541899441340782122905027932960893854748603351955307262569832402234636871508379888268156424581
1/181	005524861878453038674033149171270718232044198895027624309392265193370165745856353591160220994475138121546961325966850828729281767955801104972375690607734806629834254143646408839779
1/193	005181347150259067357512953367875647668393782383419689119170984455958549222797927461139896373056994818652849740932642487046632124352331606217616580310880829015544041450777202072538860103626943
1/223	004484304932735426008968609865470852017937219730941704035874439461883408071748878923766816143497757847533632286995515695067264573991031390134529147982062780269058295964125560538116591928251121076233183856502242152466367713
1/229	004366812227074235807860262008733624454148471615720524017467248908296943231441048034934497816593886462882096069868995633187772925764192139737991266375545851528384279475982532751091703056768558951965065502183406113537117903930131
1/233	0042918454935622317596566523605150214592274678111587982832618025751072961373390557939914163090128755364806866952789699570815450643776824034334763948497854077253218884120171673819742489270386266094420600858369098712446351931330472103
1/257	0038910505836575875486381322957198443579766536964980544747081712062256809338521400778210116731517509727626459143968871595330739299610894941634241245136186770428015564202334630350194552529182879377431906614785992217898832684824902723735408560311284046692607
1/263	0038022813688212927756653992395437262357414448669201520912547528517110266159695817490494296577946768060836501901140684410646387832699619771863117870722433460076045627376425855513307984790874524714828897338403041825095057034220532319391634980988593155893536121673
1/269	0037174721189591078066914498141263940520446096654275092936802973977695167286245353159851301115241635687732342007434944237918215613382899628252788104089219330855018587360594795539033457249070631970260223048327137546468401486988847583643122676579925650557620817843866171
1/313	003194888178913738019169329073482428115015974440894568690095846645367412140575079872204472843450479233226837060702875399361022364217252396166134185303514376996805111821086261980830670926517571884984025559105431309904153354632587859424920127795527156549520766773162939297124600638977635782747603833865814696485623
1/337	002967359050445103857566765578635014836795252225519287833827893175074183976261127596439169139465875370919881305637982195845697329376854599406528189910979228486646884272997032640949554896142433234421364985163204747774480712166172106824925816023738872403560830860534124629080118694362017804154302670623145400593471810089020771513353115727
1/367	002724795640326975476839237057220708446866485013623978201634877384196185286103542234332425068119891008174386920980926430517711171662125340599455040871934604904632152588555858310626702997275204359673024523160762942779291553133514986376021798365122615803814713896457765667574931880108991825613079019073569482288828337874659400544959128065395095367847411444141689373297
1/379	002638522427440633245382585751978891820580474934036939313984168865435356200527704485488126649076517150395778364116094986807387862796833773087071240105540897097625329815303430079155672823218997361477572559366754617414248021108179419525065963060686015831134564643799472295514511873350923482849604221635883905013192612137203166226912928759894459102902374670184696569920844327176781
1/383	0026109660574412532637075718015665796344647519582245430809399477806788511749347258485639686684073107049608355091383812010443864229765013054830287206266318537859007832898172323759791122715404699738903394255874673629242819843342036553524804177545691906005221932114882506527415143603133159268929503916449086161879895561357702349869451697127937336814621409921671018276762402088772845953
1/389	0025706940874035989717223650385604113110539845758354755784061696658097686375321336760925449871465295629820051413881748071979434447300771208226221079691516709511568123393316195372750642673521850899742930591259640102827763496143958868894601542416452442159383033419023136246786632390745501285347043701799485861182519280205655526992287917737789203084832904884318766066838046272493573264781491
1/419	0023866348448687350835322195704057279236276849642004773269689737470167064439140811455847255369928400954653937947494033412887828162291169451073985680190930787589498806682577565632458233890214797136038186157517899761336515513126491646778042959427207637231503579952267303102625298329355608591885441527446300715990453460620525059665871121718377088305489260143198090692124105011933174224343675417661097852028639618138424821
1/433	002309468822170900692840646651270207852193995381062355658198614318706697459584295612009237875288683602771362586605080831408775981524249422632794457274826789838337182448036951501154734411085450346420323325635103926096997690531177829099307159353348729792147806004618937644341801385681293302540415704387990762124711316397228637413394919168591224018475750577367205542725173210161662817551963048498845265588914549653579676674364896073903
1/461	0021691973969631236442516268980477223427331887201735357917570498915401301518438177874186550976138828633405639913232104121475054229934924078091106290672451193058568329718004338394793926247288503253796095444685466377440347071583514099783080260303687635574837310195227765726681127982646420824295010845986984815618221258134490238611713665943600867678958785249457700650759219088937093275488069414316702819956616052060737527114967462039045553145336225596529284164859
1/487	002053388090349075975359342915811088295687885010266940451745379876796714579055441478439425051334702258726899383983572895277207392197125256673511293634496919917864476386036960985626283367556468172484599589322381930184804928131416837782340862422997946611909650924024640657084188911704312114989733059548254620123203285420944558521560574948665297741273100616016427104722792607802874743326488706365503080082135523613963039014373716632443531827515400410677618069815195071868583162217659137577
1/491	0020366598778004073319755600814663951120162932790224032586558044806517311608961303462321792260692464358452138492871690427698574338085539714867617107942973523421588594704684317718940936863543788187372708757637474541751527494908350305498981670061099796334012219959266802443991853360488798370672097759674134419551934826883910386965376782077393075356415478615071283095723014256619144602851323828920570264765784114052953156822810590631364562118126272912423625254582484725050916496945010183299389
1/499	002004008016032064128256513026052104208416833667334669338677354709418837675350701402805611222444889779559118236472945891783567134268537074148296593186372745490981963927855711422845691382765531062124248496993987975951903807615230460921843687374749498997995991983967935871743486973947895791583166332665330661322645290581162324649298597194388777555110220440881763527054108216432865731462925851703406813627254509018036072144288577154308617234468937875751503006012024048096192384769539078156312625250501

简化代码并扩大计算量搜索后，得到 100 万以内的走马灯数分布：

const n_devide_len = (n) => {
    let a = 1, pool = new Set()
    while (true) {
        a = a % n * 10
        if (a == 0) { return 0 }
        if (pool.has(a)) { return pool.size } else { pool.add(a) }
    }
}

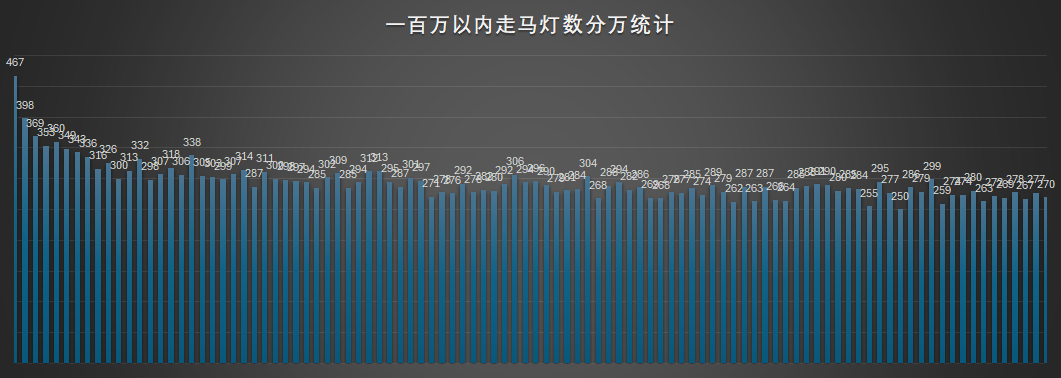
有点意思。

---

研究原因

对于任意由 1/n 形成的循环小数，$\frac{1}{n} = 0.\overline{******}$，设循环节部分为 $r$，其长度为 $l$，都可以写成一个无穷级数之和：

$$\frac{1}{n} = \frac{r}{10^l}+\frac{r}{10^{2l}}+\cdots+\frac{r}{10^{kl}} +\cdots = \sum_{k=1}^\infty\frac{r}{10^{kl}}$$

对这个无穷等比数列重新求和，$S=1/n$，$10^l * S-S = r$，得到 $S = \frac{r}{10^l-1} = \frac{1}{n}$，所以 $n=\frac{10^l - 1}{r}$ ，或者写成 $r=\frac{\overbrace{999\cdots999}^l}{n}$，这里的 r 一定是整数。这个方法同时也是将循环小数化为分数的标准方法。

• 当 $n = 7, l = 6$ 时，也就得到了 $142857 = \frac{\overbrace{999999}^6}{7}$，所以 $1/7 = 0.\overline{142857}$

• 当 $n = 3, l = 2$ 时，得到 $r = \frac{99}{3} = 33$，所以 $1/3 = 0.\overline{33}$，逻辑上其实也是对的，只是一般来说小数循环时只考虑最小周期，所以正确的写法应该是 $1/3 = 0.\overline{3}$。

• 当 $n = 11, l= 10$ 时，得到 $r = \frac{9999999999}{11} = 0909090909$，要注意这是循环节的计算因此首位的 0 不能去掉，所以 $1/11 = 0.\overline{0909090909}$，正写为 $1/11=0.\overline{09}$

对于 $1/6 = 0.1\overline{6}$ 这类存在非循环小数部分的，可以通过乘 10 等操作，把非循环部分移到整数上并抛弃，即化为 $10/6 \rightarrow 4/6 = 2/3 = 0.\overline{6}$，考察 $0.\overline{6}$ 即可。

同余

在上述 $n=3, n=11$ 两个例子中，虽然得到了逻辑上可行的循环节，但不符合通常的习惯，于在结果上进行了缩减，变为符合习惯的最小循环节。

• $10^k-1$ 本身就是 3 的倍数，所以循环节永远只有一位。

• 11 因其自身的特殊性质，11 = 10 + 1，天然地符合 10 为底的级数的结构，如果一个数字各位数值相同，那么奇数位数字对 11 都是同余的，偶数位也是。所以 $10^k-1 (mod\ 11)$ 只有两个结果 9 和 0。并且在两者间不断跳转。

可见，循环节长度即是最早出现同余时的 k 值，若要 1/n 的循环节长度为 n-1，需要 $10^k \ mod\ n$ 在 $k = 1, \cdots, n-1$ 时都不同余。

进制

从上可见，循环小数与进制密切相关。例如在 8 进制中，9（在 8 进制中也写为 11）的性质将和 10 进制中的 11 相似，也会出现奇位同余偶位同余的情况。所以 $1/11_{(8)} = 0.\overline{07}_{(8)}$，形式上完全一致。

而 $1/7_{(8)}$ 则变为了 $0.\overline{1}_{(8)}$，因为 $8^k-1_{(8)} = {\overbrace{77\dots7}^{k}}_{(8)}$ 各位恒为 7，也就不存在什么神秘数字循环了。

由于和进制本身高度相关，因此某个 1/n 是否有 n-1 位循环节，取决于它和进制 $R^k - 1$ 之间的相除结果，这个关系不知道数论中是否已有结论。

推论

1. n-1 位循环节天然存在，只是因为有可能内部重复导致长度缩减。而在 n-1 基础上的缩减不会破坏原有模式，因此最小循环节长度一定是 n-1 的因数。

2. 只有当 n 为素数时，才有可能实际出现 n-1 位循环节。由于余数需要遍历 1 到 n-1 的所有数。若 n = pq，余数会在 q-1 与 p-1 的共同作用下循环，但 p-1 与 q-1 至少含有公因素 2，不可能产生所有 {0, p-1} 与 {0, q-1} 之间的全部两两组合。

3. 一切循环节在若干次乘 10 排除不循环部分，整理为 $0.\overline{******}$ 形式后，都可以用 $a * 1/n$ 来表示。

4. 如果 n 为素数，而其循环节长度 $l$ 不为 n-1，则必有互相不能抵达的 $\frac{n-1}{l}$ 套循环，进入哪套循环取决于分子 $a$ 的值。因为素数没有因数，$a/n (a=1, 2,\dots, n-1)$ 必然有 n-1 个不同余数。

5. 如果 n 为素数，则 1/n 的循环节必然形如 $0.\overline{******}$，从小数点后就开始，即使起始是若干个 0 也是循环节的一部分。

6. 如果 n 是若干个不同素数乘积，则循环节长度是这些素数对应的循环节长度的最小公倍数。如果 n 是素数 p 的 k 次方时，循环节长度是 $l * p^{k-1},(p>3)$ 或 $l * p^{k-2},(p=3)$。

   $p=3$ 的特例在于 $p^2=9$ 仍然小于 10，没有触发进退位，即当 p^k 仍小于对应进制单位时，不往上叠加循环节长度。在 8 进制下就是正常的 $l*p^{k-1}$ 了。

7. 不存在比 n-1 更长的循环节。

8. 不同进制下的走马灯数具体是不一样的，例如 7 在 10 进制下是走马灯数，但在 8 进制下不是。2 在一切奇数进制下都是走马灯数，因为只要除不尽，循环节长度就至少为 1。

9. 除 2 以外，走马灯数的循环节长必度是偶数，将循环节的两段拆分后相加，一定是 $999\cdots$。例如 $1/7 = 0.\overline{142857}$，则 $142 + 857 = 999$。上述结论在其它进制下也成立，例如 8 进制下为 $777\cdots_{(8)}$。

   证明：设一个循环小数 $\frac{1}{n}$ 的循环节两段分别为 $\overline{r_1r_2}$，总长度为$2k$，则其既可以表达为

   \begin{align*} \frac{1}{n} = \frac{\overline{r_1r_2}}{10^{2k}} + \frac{\overline{r_1r_2}}{10^{4k}} + \cdots + \frac{\overline{r_1r_2}}{10^{pk}}+\cdots = \frac{\overline{r_1r_2}}{10^{2k}-1} &&(1) \end{align*}

   也可以表示为：

   \begin{align*} \frac{1}{n} =\frac{r_1}{10^k} + \frac{\overline{r_2r_1}}{10^{3k}} + \cdots + \frac{\overline{r_2r_1}}{10^{(p+1)k}}+\cdots &&(2) \end{align*}

   $(2)$ 式乘以 $10^n$ 再加 $(1)$ 式，得到：

   \begin{align*} \frac{(10^k+1)}{n} = r_1 + \frac{(r_1+r_2)(10^k+1)}{10^{2k}-1} = r_1 +\frac{r_1+r_2}{10^k-1} &&(3) \end{align*}

   再将 $(1)$ 式分子分母同除 $10^n+1$ 得到：

   \begin{align*}
   &&\frac{1}{n} = \frac{\overline{r_1r_2}}{10^{2k}-1} = \frac{\overline{r_1r_2}/(10^k+1)}{(10^{2k}-1)(10^k+1)} = \frac{\frac{\overline{r_1r_2}}{10^k+1}}{10^k-1} &&(4) \\
   \Rightarrow &&\frac{\overline{r_1r_2} * n}{10^k+1} = 10^k-1 &&(5)
   \end{align*}

   其中，$(4)$ 中分子 $\frac{\overline{r_1r_2}}{10^k+1}$ 不可能为整数，否则直接可以化简：

   \begin{align*} \frac{1}{n} = \frac{\frac{\overline{r_1r_2}}{10^k+1}}{10^k-1} = \frac{r_k}{10^k-1} &&(6) \end{align*}

   循环节长度直接由 2k 降为 k，这与之前的假设不符。因此在 $(5)$ 式中，$n$ 与 $(10^k+1)$ 必然存在公因数。而 n 为素数，则 $(10^k+1)$ 为 $n$ 的倍数。即 $(3)$ 式中 $\frac{(10^k+1)}{n}$ 为整数。

   因此，$r_1 + \frac{r_1+r_2}{10^k-1}$ 为整数。$r_1$ 本来就是提出来的前半循环节为整数，而 $\frac{r_1+r_2}{10^k-1}$ 是由两个长度为k的半循环节加和得到的分子，要求其为整数只可能是 1。所以 $r_1+r_2 = 10^k-1 = \overbrace{999\cdots}^k$

   得证。其它进制下的证明将底数 10 替换为对应进制即可。

计算程序

走马灯数搜索程序在得到以上结论后可以提升一些效率：

1. 使用 欧拉筛法，只在素数堆里进行验证。
2. 如果循环节小于 n-1，由于推论 1，则其至多 $\frac{n-1}{2}$，因此当计算到第 $\frac{n+1}{2}$ 项时，便可得出结论而不必计算后半段。

function searchCarousel(n) {

    let primes = [];
    let eularboard = new Array(n + 1).fill(true);
    let carousels = []

    const isCarousel = (p, radix = 10) => {
        let a = 1, pool = new Set(), end = (p + 1) / 2
        while (pool.size < end) {
            a = a % p * radix
            if (a == 0) { return false }
            if (pool.has(a)) { return false } else { pool.add(a) }
        }
        return true
    }

    for (let i = 2; i <= n; i++) {
        if (eularboard[i]) {
            primes.push(i);
            if (isCarousel(i)) { carousels.push(i) }
        }
        for (let j = 0; j < primes.length; j++) {
            if (i * primes[j] > n) break;           // 上限判断
            eularboard[i * primes[j]] = false;
            if (i % primes[j] === 0) break;         // 跳过本轮后续筛选
        }
    }

    return carousels
}

console.log(searchCarousel(1000))
// [7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233,  257, 263,
// 269, 313, 337, 367, 379, 383, 389, 419,  433, 461, 487, 491, 499, 503, 509, 541, 571, 577,  593, 619,
// 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983]

其它进制

根据前文继续厘清思路，在其它进制下：

• 循环节长度的度量和进制数无关，表述形式不改变数值大小，在 10 进制下若为 16，在 8 进制下就写为 20，但都指的是同一个值。
• 但循环节的生成和进制有关，在当前位下不满足该进制条件下的整除，产生余数，就会退到下一位。
• 在其它进制下，$r = \frac{R^{n-1}-1}{n}$ 仍然成立，这是循环小数定义公式的变形。
• 仍然只需要在素数表中搜索走马灯数，因为 r 需要由 $n-1$ 个不同余的结果来确保循环长度上限。

/* 计算各进制下的走马灯数 */
function searchCarousel(n) {
    let primes = [];
    let eularboard = new Array(n + 1).fill(true);
    for (let i = 2; i <= n; i++) {
        if (eularboard[i]) { primes.push(i) }
        for (let j = 0; j < primes.length; j++) {
            if (i * primes[j] > n) break;           // 上限判断
            eularboard[i * primes[j]] = false;
            if (i % primes[j] === 0) break;         // 跳过本轮后续筛选
        }
    }

    const isCarousel = (p, radix = 10) => {
        if (p === 2 && radix % 2 !== 0) return true // 2 在奇数进制下必然是 1 位循环
        let a = 1, pool = new Set(), end = (p + 1) / 2
        while (pool.size < end) {
            a = a % p * radix
            if (a == 0) { return false }
            if (pool.has(a)) { return false } else { pool.add(a) }
        }
        return true
    }

    for (thisRadix = 2; thisRadix < 100; thisRadix++) {
        let carousels = []
        for (let i = 0; i < primes.length; i++) {
            if (isCarousel(primes[i], thisRadix)) { carousels.push(primes[i]) }
        }
        console.log(thisRadix, carousels.length)
    }
}
searchCarousel(10000)

搜索在各不同进制下， 10000 以内的走马灯数的数量，结果如下：

进制	走马灯数数量	进制	走马灯数数量	进制	走马灯数数量	进制	走马灯数数量	进制	走马灯数数量
		21	447	41	460	61	457	81	1
2	470	22	472	42	476	62	482	82	455
3	477	23	459	43	490	63	457	83	453
4	0	24	461	44	460	64	0	84	466
5	493	25	1	45	483	65	477	85	468
6	470	26	455	46	445	66	469	86	464
7	466	27	278	47	477	67	471	87	478
8	277	28	451	48	468	68	459	88	454
9	1	29	465	49	1	69	461	89	470
10	467	30	488	50	471	70	473	90	478
11	444	31	469	51	471	71	471	91	453
12	459	32	372	52	460	72	470	92	464
13	458	33	474	53	470	73	465	93	446
14	459	34	473	54	471	74	447	94	485
15	454	35	461	55	486	75	471	95	462
16	0	36	0	56	461	76	467	96	464
17	451	37	466	57	451	77	449	97	471
18	472	38	466	58	478	78	451	98	459
19	473	39	489	59	465	79	466	99	476
20	487	40	458	60	455	80	490	100	0

这里最有特点的是当进制为偶数的完全平方时，没有走马灯数，当进制为奇数的完全平方时，只有唯一一个走马灯数 2，循环节长度为 1。

特殊进制 $R=s^2$

无论在哪种进制下，循环节公式 $r = \frac{R^{n-1}-1}{n}$ 都仍然是成立的。其中 $R$ 为指定的进制数，$n$ 为测试数字， $r$ 为对应的循环节。根据前文所述，在一些情况下循环节会缩减。即当 r 的数字序列内部出现重复时，需要用更短的循环节代替。前文 $\frac{1}{11} = 0.\overline{0909090909} = 0.\overline{09}$ 便是例子。

而当 $R$ 为完全平方数 $s^2$ 时，将循环节公式展开为；

$$ r_{(R)} = \frac{(s^2)^{n-1}-1}{n} = \frac{(s^{n-1}+1)(s^{n-1}-1)}{n} = (s^{n-1}+1) \cdot \frac{s^{n-1}-1}{n}$$

因为 $s$ 是整数，注意到 $\frac{s^{n-1}-1}{n}$ 实际上是在 $s$ 进制下的 $\frac{1}{n}$ 的循环节表达式 $r_{s(s)}$，必定是有整数解的，并且在 $s$ 进制下的长度至多为 $n-1$ 。

现在将 $r_{s}$ 的数值从 $s$ 进制转到 $R$ 进制。因为$R=s^2$，$R$ 进制下一位数值可以容纳 $s$ 进制下两位。其长度在转换后正好一半 $\frac{n-1}{2}$，n 为素数。则：

$$r_{(R)} =(s^{n-1} + 1) * r_{s(s)} \overset{s\rightarrow R}{=\!=\!=} (R^{\frac{n-1}{2}} + 1) * r_{s(R)}$$

除 2 以外的 n 都是素数，所以 $\frac{n-1}{2}$ 是整数，$(R^{\frac{n-1}{2}} + 1)$ 是形如 $\overbrace{100\cdots01}^{(n+1)/2}$ 的整数，长度上正好使 $r_{s(R)}$ 重复两遍，而不会有叠加进位。

因此当进制 $R$ 为完全平方数时，任意 $n$ 的 $r_{(R)} = \frac{R^{n-1}-1}{n}$ 数字序列至少会内部重复一次，所以长度一定小于 $n-1$，也就不存在跑马灯数。

推论：当进制 $R=s^{(2^n)}$ 时，对应的最长循环节为 $\frac{n-1}{2^n}$ 向上取整。

费马小定律

在前文中数次使用 $r=(R^{n-1}-1)/n$，并且认定它是整数，是因为该式是从循环节的级数表示法计算出来的，而循环节本身一定是 n-1 位的整数，所以认为是整数。这个推论是单薄的，不能证明任意 $(R^{n-1}-1)/n$ 一定是整数。但其实关于这一点的正向证明早就在三百多年前就被书空白写不下学家完成了：

$(R^{n-1}-1)/n$ 为整数，其实本身就是 费马小定理 的一部分，即：

• 假如 $a$ 是整数，$p$ 是素数，那么 $a^p \equiv a (mod\ p)$
• 如果 $a$ 不是 $p$ 的倍数，则 $a^{p-1} \equiv 1 (mod\ p)$，这其实就是我们用的循环节公式。
• 如果 $a$ 是 $p$ 的倍数，则 $a^{p-1} \equiv 0 (mod\ p)$，这时就除尽不构成循环节了。

我们之前提到，进制的转换会影响循环节数字序列的变化，但不影响素数、整除等基于数本身的性质，因此这里的 R 在整除判定上反而和进制本身没什么关系，就是一个单纯的幂底数。

模运算与原根

当引入费马小定律后，我们进入了数论中模运算的领域。在前文中有一条推论 2：

只有当 n 为素数时，才有可能出现 n-1 位循环节。由于余数需要遍历 1 到 n-1 的所有数。若 n = pq，余数会在 q-1 与 p-1 的共同作用下循环，但 p-1 与 q-1 至少含有公因素 2，不可能产生所有 {0, p-1} 与 {0, q-1} 之间的全部两两组合。

其实是在数论的门外匆匆一瞥。思而不学则民科，在查询了一些资料后，发现其实这些走马灯数在数论中早已有深入的讨论。本文前半篇是从计算中发现现象，再从现象中思索原因。后半篇打算从原理出发，厘清前因后果全套链条。

欧拉函数 ϕ(n)

为了循序渐进，先来熟悉一下欧拉函数，其定义为：

$$\phi(n)=小于正整数 n 且与 n 互素（即最大公约数为1）的正整数的个数。$$

注意这些正整数不一定是素数，例如 8 与 9 是互素的，但两个都不是素数。

这个函数描述相比一般函数通俗得多，这也是数论领域的特色。尽管如此，这个函数实际上却并不用真的去逐个数个数，它确实是有公式通解的：

一般地，若 $n=p_1^{k_1}\cdot p_2^{k_2}\cdot \cdots \cdot p_m^{k_m}$，$p_m$为 n 的素因数，则：
$$\phi(n)=n\cdot\left(1-\frac{1}{p_1}\right)\left(1-\frac{1}{p_2}\right)\cdots\left(1-\frac{1}{p_m}\right)$$

• 当 n 为素数时，所有 $1\leq k < n$ 均有效，$\phi(7)=7-1=6.$
• 当 $n=p^k$ 为单一素数的幂时，, $\phi(8)=\phi(2^3)=2^3-2^2=4.$

欧拉公式便是上文 推论6 的完整表述。略一思索也可以很快得出结论：『互素』其实就要求所有数都『避开』n 的所有素因数及其构成的合数集，这其实就是个变形的组合数与容斥问题，形式上类似于：

$$\phi(n)=n -\sum{\frac{n}{p_i}} + \sum{\frac{n}{p_ip_j}} - \sum{\frac{n}{p_ip_jp_k}} + \cdots + (-1)^{m-1}\frac{n}{p_1p_2\cdots p_m}$$

整理便可得到通项公式。

另外值得注意的是，欧拉公式中并没有显式地使用到幂数 $k_1 \cdots k_m$，实际上是因为 $n=p_1^{k_1}\cdot p_2^{k_2}\cdot \cdots \cdot p_m^{k_m}$ 中已经包含了所有的 $k$。

整数环与有限域

在模运算 $\ mod\ n$ 中，所有余数相同的整数都被视为等价的，即 $a+kn \equiv a \ mod\ n$，通常用最小非负余数 $[0],[1],[2],…,[n−1]$ 表示这些等价类。所有的余数类构成一个集合，称之为 n 的整数环，用奇怪符号 $\Bbb{Z}/n\Bbb{Z}$ 表示。

整数环也有类似一般逻辑的『加法』与『乘法』运算：

$$[a]+[b]=[a+b]\ (mod\ n)$$
$$[a]\cdot[b]=([a] \times [b])\ (mod\ n)$$

从进制的角度也很好理解，大于 n 的部分『进位』上去了，无法影响最后一位余数的运算。尽管模运算本身没有提到进制，但进制本身就是模的一种应用，通过两者的相似性有助于理解问题。

因为同余的是一类数而不是一个数，因此没法直接做除法运算，但可以定义一个 乘法逆元，当：

$$[a] \times [b] \equiv 1 \ mod\ n$$

时，$[a]$ 与 $[b]$ 就互为乘法逆元。

同样地，和乘法中 0 类似，模运算也会出现 $a \times b \equiv 0 \ mod\ n$ 的情况，零因子没有逆元。出现零因子的原因也很简单，当 n 为合数时，a b 两个非零元素相乘后结果能被 n 整除。

整数环仅仅是个称谓，任意整数 n 都有长度为 n 的整数环，并不能体现什么特殊性。但 n 不同会使得对应的整数环内部表现出不同的性质，则是深入探究的目标。

前面也看到，有些整数环内部存在零因子，有些则没有。判断方法很简单，当 n 为素数时，其整数环内部没有零因子，所有非零同余类都有对应的乘法逆元。这就和上面的 推论2 一致了。此时整数环获得了一个新名字：有限域。

原根、欧拉定理与阶

当我们在关注循环小数的循环节时，本质上是对其不断循环取除的过程，将余数乘以进制，除以 n 以后再取余数，如此不断循环。如果将这个过程抽象一下，其实就是如下表述：

在模 n 的整数环中，对整数 $r$ 的幂次 $(r^1, r^2, \cdots, r^k)$ 不断进行模运算，则其或落入零因子，或者在一或多个非零同余间循环。

——实际上就是 r 进制下 1/n 的循环节计算过程，或者被整除，或者处于某个循环。

在数论课本中，对上述内容做了展开，有更严谨而完备的表述与证明过程：

欧拉定理

若 a 与 n 互素，则 $a^{\phi(n)} \equiv 1 \ mod\ n$

欧拉定理的证明过程大致分为四步：

1. 设模 n 的简化剩余系为 $S = {r_1, r_2, \cdots, r_{\phi(n)}}$ 满足 $gcd(r_i, n) = 1 $，且任意两项不同余，即 $r_i \not\equiv r_j$。

2. 将 $S$ 每个元素乘以 a，得到 $a\cdot S= {a\cdot r_1, a\cdot r_2, \cdots, a\cdot r_{\phi(n)}}$。此时若 $a\cdot r_i \equiv a\cdot r_j \ mod\ n$，则因 a 与 n 互素可消去，得到 $r_i \equiv r_j$，矛盾。 故 $a\cdot S$ 仍为简化剩余系，与 $S$ 包含相同的剩余类，仅顺序不同。

3. 由于两者同余，$S$ 和 $a\cdot S$ 的乘积相等：

   $$\prod_{i=1}^{\phi(n)} r_i \equiv P\ mod\ n \equiv a^{\phi(n)} \cdot P\ mod\ n \equiv \prod_{i=1}^{\phi(n)} (a \cdot r_i) $$

4. 由于 $P$ 是乘积，$r_i$ 与 n 互素，故 $P$ 也与 n 互素，两边同乘 $P$ 的逆元 $P^{-1}$，得到 $ a^{\phi(n)}\equiv 1 \ mod\ n$

阶与原根

由欧拉定理，可以定义 阶 与 原根：

1. $a$ 和 $n$ 为互素的正整数，则 $a$ 模 $n$ 的阶是满足 $a^k \equiv 1\ mod\ n$ 的最小正整数 $k$。
2. 若整数 a 与 n 互素，且其模 n 的乘法阶数等于 ϕ(n)，则称 a 是模 n 的一个原根。

或者使用另一个等效表述：

在模 n 的整数环中，若存在整数 $a$ 使得 $(a^1, a^2, \cdots, a^{\phi(n)})$ 能够遍历所有与 n 互素的剩余类，则 $a$ 称为模 n 的一个原根。

一次能遍历所有可能的余数，也就是循环节达到了最大值，这个最大值就是欧拉函数 $\phi(n)$。存在原根和最长循环是一体两面的。

应用

进一步地，若要 $\phi(n) = n-1$ 则 n 必须是素数，也就是说，走马灯数的分母 n 必须是素数。而当 $n=p $（素数）时，$\phi(n)=p-1$，欧拉定理简化为：$a^{p-1}\equiv 1 \ mod\ p $，这就是费马小定理！

到这里，就和前文的推论 2, 6, 7, 8 都对上了，甚至进一步地和 1, 4 也都能对上，一切全联系起来了！甚至我们还发现了之前没有注意到的 推论10：n 可能有多个原根，则 1/n 可能在多个进制下有循环小数，并且所有可能的进制下，循环节的长度都是一样的。

接下来就是在欧拉定理的指导下，科学地判定走马灯数了：

1. 当 $n = 1, 2, 4, p^k, 2p^k$ 时存在原根，且阶为 $\phi(n)$。但只有 $\phi(n) = n - 1$ 时才能称为『走马灯数』，所以 n 必须是素数。
2. 当且仅当 $a^{n-1} \equiv 1\ mod\ n$ 时，a 即为原根，对应的 n-1 即为循环节长度。
3. 只需排查任意 $n-1$ 的真因子 $d$ 是否会使得 $a^d \equiv 1\ mod\ n$，如果有，则 $a$ 不是 $n$ 的原根。

程序优化

1. 添加 n-1 的真因子 d 的计算过程，这是个因式分解过程。考虑到我们之前已经计算出了素数表用于 n 的选择，这里可以复用。
2. 在实际计算中，$a^{\phi(n)}$ 仍然是个巨大的数，容易有溢出风险，但模运算支持乘法，因此可以把 $a^b\ mod\ n$ 的指数$b$拆分求模：
   $$((a\ mod\ n )^{b_1} \times (a\ mod\ n )^{b_2} \times \cdots \times (a\ mod\ n )^{b_k})\ mod\ n$$
3. 只验证所有 d 下 $a^d \not\equiv 1\ mod\ n$，有 false 直接退出。即排除推论4 描述的情况。

据此我们写出了最终的走马灯数快速算法，直接应用欧拉定理，分解 n-1 的素因数，代替原来的试除法进行验证，并使用模运算的乘法分解式来计算 $a^b$ 以避免大数问题。这个算法在 n 较大时的效率比原来有了很大提升。旧算法搜索 100万以内的走马灯数约需20分钟，新算法不到 1 秒，提升了 1000 倍。

function searchCarousel(n, radix = 10) {

    let primes = [];
    let eularboard = new Array(n + 1).fill(true);
    let result = []

    // 去重列举 n 的所有素因数
    function primeFactors(n) {
        const factors = new Set();
        let i = 0;
        while (n > 1 && primes[i] < n) {
            while (n % primes[i] === 0) {
                factors.add(primes[i])
                n = n / primes[i];
            }
            i++
        }
        if (n > 1) factors.add(n)
        return Array.from(factors);
    }

    // 计算 a^b mod n 的值
    function modExp(a, b, mod) {
        let result = 1n;
        a = BigInt(a) % BigInt(mod);
        b = BigInt(b);
        mod = BigInt(mod);
        while (b > 0n) {
            if (b % 2n === 1n) { result = (result * a) % mod }
            a = (a * a) % mod;
            b = b / 2n;
        }
        return Number(result);
    }

    // 判断是否为全循环质数（原根验证法）
    function isCarousel(p, radix) {
        const phi = p - 1; 
        if (modExp(radix, phi, p) !== 1) return false; // 费马小定理
        const factors = primeFactors(phi);
        for (const factor of factors) {
            const d = phi / factor // 因为 factor 是独立最小素因数，使用对应的 d 可以最大化否决。
            if (modExp(radix, d, p) === 1) return false;
        }
        return true;
    }

    // 欧拉筛获得素数表
    for (let i = 2; i <= n; i++) {
        if (eularboard[i]) {
            primes.push(i);
            if (isCarousel(i, radix)) { result.push(i) }
        }
        for (let j = 0; j < primes.length; j++) {
            if (i * primes[j] > n) break;           // 上限判断
            eularboard[i * primes[j]] = false;
            if (i % primes[j] === 0) break;         // 跳过本轮后续筛选
        }
    }

    return result
}

console.log(searchCarousel(1000000))
//[ 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383,
// 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887,
// 937, 941, 953, 971, 977, 983, 1019, 1021, 1033, 1051, 1063, 1069, 1087, 1091, 1097, 1103, 1109, 1153, 1171, 1181, 1193, 1217, 1223,
// 1229, 1259, 1291, 1297, 1301, 1303, 1327, 1367, 1381, 1429, 1433, 1447, 1487, 1531, 1543, 1549, 1553, 1567, 1571, 1579, 1583, 1607, 1619, 
//...29400 more items]

进一步地，搜索非 10 原根即非 10 进制下的走马灯数时，除了 n 质数这一条件不变之外，其它也有一些应用定理可以优化的点：

1. 若 $g$ 的阶为 $\phi(n)$，则 $g^k$ 的阶为 $\frac{\phi(n)}{gcd(k,\phi(n))}$
2. 当且仅当 $gcd(k,\phi(n)) = 1$ 时，$g^k$ 的阶仍为 $\phi(n)$

故，假设 $g$ 是模 n 的一个原根，则所有其它原根可表示为 $g^k\ mod\ n$，其中 $gcd(k,\phi(n))=1$

所以算法上，应当从 $g=2$ 开始搜索第一个原根，先与 n 做互素判定，再应用上文的 isCarousel() 函数。找到 $g$ 后，再寻找 $k$ 令 $gcd(k,\phi(n))=1$，则其它原根即为 $g^k\ mod\ n$。gcd() 函数的计算比 modExp() 函数更高效。

• 以 n = 7 为例，$\phi(7) = 6$，
• 搜索到第一个 $g=3$，$3^6 \equiv 1\ mod\ 7$，且验证了 $3^2 \not\equiv 1\ mod 7$ 和 $3^3 \not\equiv 1\ mod 7$，所以 3 是原根。
• 搜索 $k$ 使 $gcd(k,6)=1$，且 $1<k<6$，有唯一解 $k=5$，计算 $3^{k=5}\ mod\ 7$，madExp(3,5,7) == 5，即 5 为第二个原根。注意 $g_2=5$ 与 $k=5$ 是两个独立的计算过程，虽然值一样。
• 对于其它进制，例如 7 应当在 10 进制下也是 6 位循环，是因为 $10\ mod\ 7 \equiv 3\ mod\ 7$。若要在程序的输出结果上体现出来更大的进制，只需要输出前加个循环即可。

// 代码暂略，有空再写