计算机里的随机数

发表于 2016-07-31 分类于硬用数学

计算机中没有随机数。

本文完。

小游戏里的小随机

如果做个打地鼠小游戏，要让地鼠从 9 个小洞里『随机』出现，不能挨个洞出来。简单办法是给九个小洞编上号 0-8，然后令 Hole_n+1 = (4 * Hole_n + 4) mod 9。也就是乘4加4，然后除 9 取余数。游戏开始，我们希望地鼠第一次从中间的洞，也就是4号洞里出来。所以 Hole₁=4。得到的结果是：

1	4,2,3,7,5,6,1,8,0,4,2,3,7,5,6,1,8,0,4,2,3,7,5,6,1,8,0,……

也就是地鼠会这样出现：

mouse

看起来很规律，记一记就记住了。但把上面公式的几个常数放大，变成 X_n+1 = (1103515245 * X_n + 12345) mod 2³¹，序列就变成了：

4,119106029,1583775792,1104372736,1199162368,546350080,1200489472,1420813312,2119975936,33629184,192185400,1547013152,339646976,1301529152,177825024,1578512704,703899648,1482405888,1629325312,151197696,1470195776,1593643776,1066092288,1743743744,1972027136,205882112,964884288,1603859968,320138752,342722112,654956928,……

数字太大，做一下归一化。因为是 mod 2³¹的结果序列，所以归一化也就是除以 2³¹，得到：

0.0000000019
0.0554630668
0.7375030741
0.5142636299
0.5584034920
0.2544140816
0.5590214729
0.6616177559
0.9871907234
0.0156598091
0.0894933008
0.7203841358
0.1581604481
0.6060717404
0.0828062296
0.7350522578
0.3277788162
0.6902990341
0.7587137222
0.0704069138
0.6846132576
0.7420982122
0.4964379072
0.8119939566
0.9182966948
0.0958713293
0.4493092597
0.7468554974
0.1490762234
0.1595924199
0.3049880862
…………

我们再次把这个序列处理回地鼠出现的序列，Floor(X_n*9)，得到：

1	0,0,6,4,5,2,5,5,8,0,0,6,1,5,0,6,2,6,6,0,6,6,4,7,8,0,4,6,1,1,2,……

来 1000 个：

0,0,6,4,5,2,5,5,8,0,0,6,1,5,0,6,2,6,6,0,6,6,4,7,8,0,4,6,1,1,2,6,4,1,2,0,2,3,1,1,6,6,4,6,4,5,2,3,8,0,7,8,4,3,0,4,1,1,0,4,3,5,4,6,8,8,1,2,5,6,5,8,2,4,8,1,2,6,3,1,3,7,8,8,4,2,8,7,8,4,5,3,6,3,3,6,8,0,1,1,4,8,0,5,3,5,7,5,4,4,0,7,5,3,1,4,1,2,3,5,8,7,0,5,6,5,0,6,0,4,3,1,7,4,0,3,4,6,5,2,5,5,8,1,2,7,7,3,8,0,4,8,5,3,6,7,6,1,5,2,5,0,1,0,6,5,3,6,0,7,1,3,0,1,2,0,2,4,6,0,2,1,5,6,2,1,0,0,0,0,7,2,4,0,1,6,2,4,3,4,1,5,1,6,7,3,7,8,3,3,3,3,6,1,1,4,0,3,7,5,0,0,3,7,7,7,5,4,3,8,2,2,2,7,7,2,6,1,2,2,6,3,8,8,3,3,0,2,2,3,6,1,4,6,1,8,1,5,7,1,7,6,5,0,6,4,2,0,6,0,0,8,7,6,8,0,1,2,5,5,1,1,3,7,7,0,3,2,4,5,1,2,1,0,8,1,6,6,4,5,5,1,0,1,5,5,6,5,3,5,7,5,0,2,7,8,7,6,5,6,7,0,1,0,3,4,1,4,4,2,3,7,8,1,5,4,1,8,8,6,5,0,8,1,6,4,7,6,4,1,8,5,3,5,8,6,4,7,3,3,0,7,2,3,3,8,0,5,3,6,6,3,0,1,4,7,4,0,1,5,0,1,4,3,0,4,0,0,1,0,5,4,4,5,4,3,6,4,8,5,7,6,7,4,0,8,4,2,7,8,6,6,0,4,4,6,6,6,4,2,3,8,2,1,6,8,5,3,6,4,3,7,3,4,5,4,8,6,1,5,0,4,1,7,6,5,7,3,5,6,5,7,5,0,4,0,1,7,0,5,6,3,0,8,7,6,3,3,3,8,1,3,4,8,1,4,7,3,3,3,1,6,0,4,8,8,3,7,5,7,3,8,3,3,7,2,7,7,1,3,7,2,6,7,1,1,7,4,4,8,0,7,2,6,7,6,0,7,7,1,8,2,3,4,7,3,3,4,3,0,0,7,5,1,8,2,3,1,0,1,4,7,2,0,0,7,8,5,3,1,0,3,8,5,7,8,5,1,5,3,7,3,6,0,8,8,7,8,8,4,7,1,0,6,5,6,4,5,0,4,7,0,8,5,8,8,5,4,3,8,5,4,3,8,6,6,4,6,3,3,3,1,6,3,0,4,7,7,2,2,2,7,1,3,2,0,4,2,2,2,1,2,2,8,2,4,7,8,7,1,2,6,8,0,7,3,1,0,7,0,0,8,6,1,0,0,4,1,0,5,4,2,8,8,2,8,7,7,0,3,3,8,8,2,4,1,3,6,1,1,5,3,6,8,3,3,3,5,4,4,8,4,6,1,6,2,8,1,1,3,0,0,5,0,0,2,2,8,8,8,8,3,7,1,0,0,5,0,7,7,7,7,4,3,2,6,8,7,6,7,0,4,8,7,2,2,7,6,3,5,2,8,8,5,6,8,2,0,8,3,7,0,4,5,4,4,0,5,3,5,4,1,7,3,7,5,8,4,6,0,6,2,1,4,6,7,8,0,3,0,5,5,3,2,5,2,6,4,7,0,6,5,2,1,0,4,1,5,3,4,6,8,0,1,5,5,1,1,1,3,8,3,2,7,4,5,4,3,1,4,0,8,3,5,6,7,4,5,8,2,6,2,1,4,6,3,6,3,7,2,5,8,2,5,8,1,3,3,5,7,8,5,4,6,0,7,3,3,4,8,3,2,4,0,4,4,2,7,6,2,1,0,4,0,1,8,3,2,8,0,5,2,1,1,1,2,1,7,4,1,1,4,1,8,7,5,6,2,5,3,4,6,2,8,3,7,6,7,5,2,1,0,7,1,8,8,5,5,7,2,5,6,4,4,2,5,2,0,2,5,6,8,2,4,6,3,7,4,5,0,0,4,1,2,1,7,1,2,5,3,3,0,3,8,7,6,0,2,5,5,6,4,2,0,8,7,2,0,2,5,0,4,5,4,8,2,7,6,4,1,7,7,6,5,1,6,8,0,0,1,0,4,6,3,0,7,2,7,5,1,0,5,5,2,6,0,7,0,4,0,……

这个已经足够『随机』了，发现不了什么明显的规律，统计上也符合平均分布。要说规律也是有的，就像之前 mod 9 于是出现了 9 个一循环一样。在把常数增大以后，这个序列的循环也变成了 2³¹。

因为打地鼠游戏中的『随机』的要求，只是无法让玩家找到并掌握规律。任何一个玩家都不可能打上 2³¹ 只地鼠，所以这个算法生成的『随机』已经足够了，截取其中一段完全符合打地鼠的要求。

事实上， f_n+1 = (a * f_n+b) mod c 正是一种很传统的计算机随机数生成法，称之为线性同余法，是使用最广泛也是最古典的随机数生成算法之一。随着时代发展和实际需求不断加深，更加严格的算法被不断发展出来，但线性同余由于算法简单，计算性能高效而又能满足很大一部分一般需求，依然是大部分编程语言 rand() 函数的默认实现方式。从公式可知这些随机数并不是真正的随机，总是会在 c 的范围内循环出现。当

1
2
3

b 和 c 互素
a-1 可被所有 c 的质因数整除
如果 c 是 4 的整数倍，则 a-1 也是 4 的整数倍

时，输出序列的周期为 c。只要保证 c 足够大，那么一般情况下是不会遇到周期性重复的。

事实上 a=1103515245, b=12345, c=2³¹ 正是C语言标准函数 rand() 所使用的几个常数。rand() 函数包含于 stdlib.h 头文件库中。

种子

从算法可知，假如 X₀ 不变，那么每一次执行程序，得到的“随机数据”其实都是一样的。执行两遍程序，得到完全样同的数据，重开一次游戏，NPC 的行为一模一样，这感觉其实并不怎么好。但从数学的角度上看，既然算法是一定的，那么每一步得到的数据也必然是确定的，如果初始值相同，那么后续的值也一定是相同的。甚至即使一个序列中断了，只要后续重新设定的种子值与中断前的最后一个值一致，那么这个序列就可以原样继续下去。

换个角度看，只要用不同的初始值，我们就能得到不同的结果。

这一初始值，被称为算法的『种子』(Seed)。最常用的种子数据大概就是使用系统的当前时间了，这是一个简单易用，必然存在，而且还时时刻刻在变化的值。可以让每时每刻产生的随机序列都有所不同。稍复杂一些的有 CPU 当前温度，用户鼠标的移动轨迹，键盘的击键速度等，属于不可预测的 Seed。

『种子』这个词汇甚至不光是随机数据生成算法里有，加密解密算法、身份识别、图像算法等都有这一词汇的出现（当然下载界也有这个词）。对加密算法而言，种子数据往往是高度保密或者完全无法复现的了。前面说的鼠标键盘数据即属于此类。于是围绕种子值往往也会产生许多巧妙的奇思秒想与攻防破解，后文再述。

随机与伪随机

不光是线性同余，计算机里一切随机数生成方法实际上都是通过一定的算法生成的，区别只是在于算法复杂不复杂，种子的要求高不高，得出来的 结果能不能满足实际场景的需要。这些通过公式计算得到的“随机数”，有一个特定的名称『伪随机』(Pseudorandomness)。即，看起来像是随机的，实际却不是。但看起来随机往往就足够了。

在有些场景里，这种通过计算机生成的伪随机算法会变得无法符合真实需求。

大规模的理化生模拟实验，伪随机算法在统计上的瑕疵可能会影响到模拟实验的结果数据。

——由于实验可能会用到海量的随机数据，部分伪随机算法的规律性或者其它统计上的瑕疵正好撞上实验的检查项，就会导致实验结果的异常。
程序员开年会，了解了随机数原理的程序员们纷纷表示不能被一个确定的算法影响了自己的『强运』。

——由于对年会奖品抽奖程序的不满导致年会现场变成 Code Review 大会的事情简直随处可闻。
赌场这种胜负直接关系到利益的地方

——关于伪随机算法缺陷导致巨额损失的情况后文细讲。
涉及到窃听与加密、远程控制肉机等可能造成反复利用的情况

——往往破解出一种加密方法，就可以进入大量的服务器，产生巨大的利益。

这时人们会更倾向于使用常识中认为的『真随机数』，例如放射性衰变、电子设备的热噪音、宇宙射线的触发时间等等。比如专门提供这类服务的 random.org 网站，声称是通过测量大气噪音(Atmospheric Noise)获得的随机数据。相比于受到算法限制的数据，毕竟这些数据感觉更“随机”一些。

当然，使用环境数据，则会受到测量传感器采样率的限制，数据的生成速度会受到影响。同时，很多自然环境数据也是连续渐变，或者服从一些确定的分布，随机性可能没有预想的高。比如 CPU 温度之类，在一定时间内的变化总是一条较为连续平滑的曲线。

所以更务实的办法是混用两种情况，即使用一套设计良好的随机数生成算法，了解算法的适用场景，避开算法缺陷，同时使用环境数据作为 Seed。初始值『真随机』后，后续尽管是伪随机但也拥有了更大的不可预测性，在大量重复实验中会表现出来更多的随机性，也就有了更广泛的使用场景。

“更随机”与“不那么随机”

对『随机程度』概念的理解多少有点凭感觉。尽管数学上对随机和随机程度是有严格定义的，但引用《信息简史》里提及的，香农提出的例子，大概更容易让人理解『随机程度』的意思：

·零阶近似一一完全随机的字符，其中不存在结构或依赖：
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD
QPAAMKBZAACIBZLHJQD.

·一阶近似一一每个字符与其他字符不存在依赖关系，各自的出现频率取在英语中的出现频率：字母 e 和 t 出现得较多，而 z 和 j 较少，且单词长度看起来也较接近现实。
OCRO HLI RGWR NIMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.

·二阶近似一一不仅单个字母，双字母组合的出现频率也符合英语的情况。
(香农从密码破解者所用的表格中，找到了所需的统计数据。英语中最常出现的双字母组合是 th ，大致每千个单词出现 168 次，紧跟其后的是 he, an, re, 和 er 还有相当数量的双字母组合的出现频率为零。）
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN DILONASIVE TUCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.

三阶近似一一三字母组合也符合英语的情况。
IN NO 1ST LAT HEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.

一阶单词近似
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD BE THESE

二阶单词近似一一双单词组合以英语中期望的频率出现，所以不会出现上例中 “A IN” 或 “TO OF” 的情况。
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED

衡量随机性的方法就是香农同学提出的信息熵概念。在这里没有必要展开论述计算方法，我们使用另一个例子来简单说明随机程度：

这是一个来自知乎的巧妙方法，尽管局限性很大，但却一目了然：

random

对于通过算法生成的随机数序列而言，在整个序列中多少会存在一定程度的『局部结构』。『结构』的存在和反复出现，就表明这一序列的随机程度较差。结构越多越密，随机度越差。上面两个例子都展示了这种『结构』的存在。结构是可以预测的，可预测的越多，随机性就越少。赌徒们大概更容易理解这点吧。

生成方法与评价方法

线性同余法

线性同余法的公式非常简单，如果已知了足够长的结果序列以后，三个参数 a, b, c 也很容易反推出来。从数学上讲，任何一个可以被计算机运行的算法都必然有有限大的取值范围，既然范围有限，到最后必然会出现周期性循环。尽管如此，2³¹（大约21亿）的循环周期也小了一点。尽管没人会去打 21 亿只地鼠，但是 21 亿粒子碰撞，21 亿次装备掉落等等都是很有可能出现的。线性同余法的优点在于高效简洁易于实现，能满足常规需求，但人们还是需要更复杂更随机的算法。

Mersenne Twister

维基百科上有比较详细的论述。它的循环周期为 2¹⁹⁹³⁷ − 1，这是个梅森数所以才叫“梅森旋转”，和梅森本人大概是没啥关系。算法优点一是循环周期大，二是可以通过一些比较严苛的随机数测试，三是可以实现 1 ≤ k ≤ 623 范围内的 32 位精度 k-分布。

缺点一是速度较慢，但在现有的计算机性能下常规运算不是太大问题。二是在一些特定的初始值下，输出的序列会有大量相似模式。也就是会出现初始值相似而输出序列大量相似的情况，这个比较要命。另外，它通不过 TestU01 等少数随机测试。

Multiply with carry
MWC 是 George Marsaglia 提出的方法，优点在于速度快周期特别大，大约有 2⁶⁰ 到 2^2000000。缺点维基上没写，我猜测大概是结构较为明显，不适合的场景较多吧。OpenCV 使用了 MWC 作为随机数生成器，在图像领域，速度和周期确实是最重要的，相比之下，结构导致的缺陷并不重要且容易规避。

其它
维基百科上有专门的目录页提到了伪随机数生成器：https://en.wikipedia.org/wiki/Category:Pseudorandom_number_generators，而很显然这并不是全部的随机数生成程序。每一种伪随机算法都有自己的优点和缺点，适用于不同的场景。在一些简单场景下，设计人员也会使用更简化的，可以通过互质齿轮组机械结构实现的随机，比如：

98aed764834fb9165ced3945b6bc87b2_b

算法评价

同时，当然也有各种针对伪随机数测试方法，去检验生成数据的质量（即随机性如何）。原理基本都是评测生成的序列是否符合必要的复杂性要求。这与无损压缩算法反而有某种异曲同工之处，毕竟压缩算法的目的就是寻找规律模式并且使用更短的片段去代替它。几乎所有的随机序列测试都是基于假设检验、广义傅立叶变换和复杂性测试，对一个已经生成的伪随机数序列进行检测，寻找模式，并评测结果。

最简单的理解，如果你用 int(rand(0,255)) 一百万次生成了一个 .bin 文件，扔进 Winzip 里，结果体积压缩了一半，那么这个随机数生成算法就是非常不合格的。这跟上面的点阵图方式很相似。

顺便附上还是从知乎同一问题下抄来的四原则：

K1——相同序列的概率非常低
K2——符合统计学的平均性，比如所有数字出现概率应该相同，卡方检验应该能通过，超长游程长度概略应该非常小，自相关应该只有一个尖峰，任何长度的同一数字之后别的数字出现概率应该仍然是相等的等等
K3——不应该能够从一段序列猜测出随机数发生器的工作状态或者下一个随机数
K4——不应该从随机数发生器的状态能猜测出随机数发生器以前的工作状态

作者：DD YY
链接：https://www.zhihu.com/question/20222653/answer/16482344
来源：知乎

说实话这四条只是原则，并不是任何一个实测的测试方法。单一的测试方法也无法涵盖各种可能性，所以一些比较有名的测试，Diehard Test、TestU01 等实际上都是测试包，包含了多种不同的方法，尽可能覆盖测试的方方面面。

回到游戏

计算机程序大部分都服务于确定的目的，不会有随机的成分存在。查字典不可能随机给解释，打字不可能随机出字，做帐目不可能随机变计算结果。那么什么地方需要随机？最常见的也就是游戏了，包括电子赌博。所以再回来说说游戏中的随机。

『乱步』

圆桌武士(Knight of the Round) 是个当年非常受欢迎的街机游戏，应该也是不少人的童年回忆。

knights001

这款游戏后来被有心人研究出来被发现者命名为『乱步』的方法，类似以下这些规则：

1.红色小兵（不戴头盔的，血少）
a.砍开箱子出 800 分宝箱，他在地上滚动的时候，砍开 800 分，出魔杖。
b.屏幕上如果有两个桶，先不开桶，等他在地上滚的时候，放血放死他，然后开另一个桶，再开 800 分的桶，再开 800 分，出魔杖。
2.绿色小兵（戴头盔的）
a.先吸引他跑动(不攻击)，如果他马上又跑动攻击的话，出刀时放血放倒但不要放死他，马上去开箱子。等他站起来踹气的时候，开 400 分或蔬菜盘，出地震法球(这种方法不能出杖，up)。
b.在他在地上滚动时，放血放死他，然后开一个箱子，开里面的分或血，再开 800 箱子，开 800 分，出魔杖。
3.胖子(Fatman)
a.走 C 步时( C 形状的步子，步子很小也很快，就那么一下)，放血放倒他，马上开箱子，在他起来踹气时开800分，出魔杖。
b.站在他前方等他冲跑过来攻击你，他冲的时候你马上站在他斜下的方向，他如果走向下走一步（只是1步），放血放死他，然后开两个箱子，再砍 800 分，出魔杖。
4.大剑(Swordman)
a.同样是观察它走 C 步，放血放倒它，马上砍 800 箱子，等它站起来就开 800 分，出魔杖。
…………

乱步的实质就是随机数规律被人掌握了。

受限于街机主板不高的性能，游戏开发使用了比较简单的一个随机数发生器，实际的重复周期很小。同时还将宝物掉落、敌兵行动、主角行动等一系列需要随机的行为，全放在同一个随机数序列中。每一个需要随机的行为，都让这个序列往后走一格，一轮序列走完再从头开始第二轮。

也是因此，玩家可以通过反复的的跳跃、放血大招等动作，来『快进』掉随机数序列中的若干位数字，到需要的位置，再劈砍宝箱，以获得指定的需要的宝物。如下图，当随机序列进行到 03 时，游戏中某个小兵根据该数字进行了冲锋动作，使用掉 03 这个数值。序列进行到 1C，被玩家用连续两次跳跃消耗掉两个随机数，使得随机序列当前值变为 0F。而 0F 对应于掉宝则为『魔杖』。

即，用户根据一些游戏内的特别现象，通过自己的操作控制了掉宝内容。

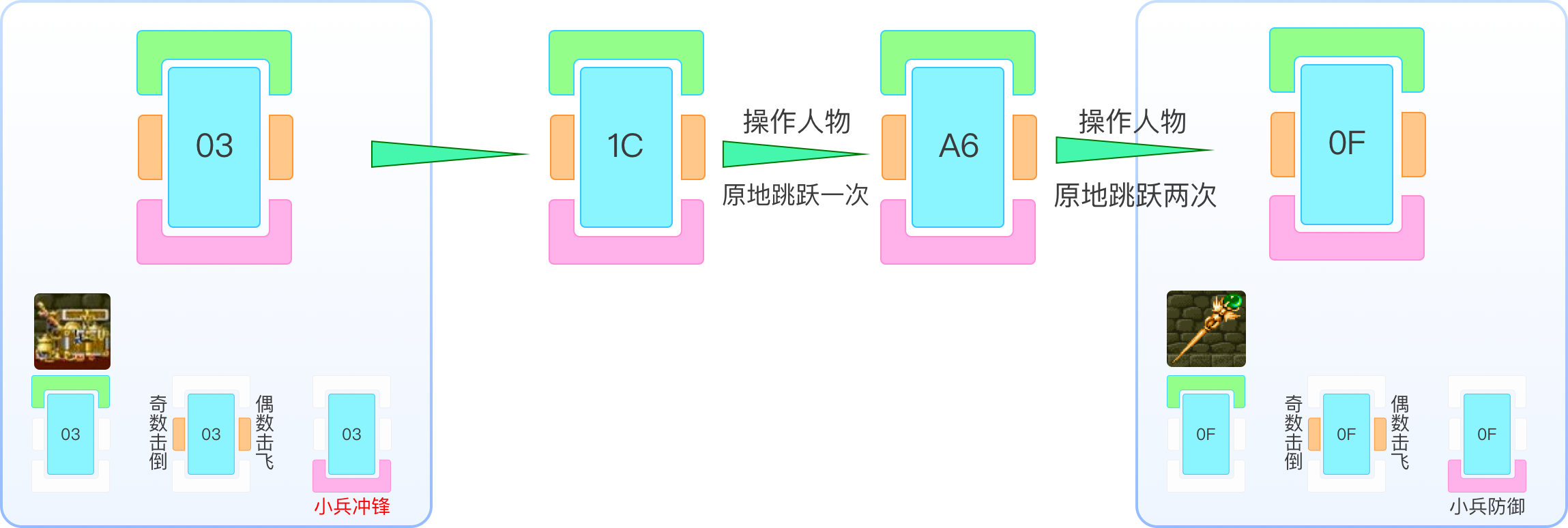
ranbu

可是主角行动是个受玩家操控的行为，并不是一个需要随机的东西，为什么还会在随机序列中并影响到掉宝结果？

有两个原因。一是为了让画面更富有表现力，游戏主角的动作会有多种画面表现。同样是跳，可以表现为前空翻跳，直立跳。同样是转身，一种先转头，一种先迈步，等等。而另一个原因仅仅是为了让序列更随机。没错，就像前文写过的那样，使用键盘击键、鼠标轨迹等算法外部的影响因素，可以让破解者更难以发现规律。当然，也可能两个原因都有。

我猜测圆桌武士这个游戏就是第二类情况。由于玩家行动，尤其是多人游戏，多位玩家同时行动时，玩家行为的不可预测性甚至比有限机能下内部的随机数发生器更有效，这可以避免简单地被玩家发现『如果做了 A 接下来一定是B』的规律，也避免了敌人行动永远一致的囧境。事实上在它的游戏生命周期内，几乎是整个街机的商业周期内，都运作得很好。直到电脑模拟器时代，才由几个多年孜孜不倦研究的玩家发现并完善了这份随机表。

看起来，似乎让玩家动作可以影响随机序列是个坏主意，若玩家掌握规律，岂不是就可以通过自身动作来影响游戏掉宝等结果了么？但事实并非如此。『并非如此』不是说不影响结果，而是说在玩家动作里设置锚点以影响随机数序列，进而影响掉宝，并不是一个坏主意。

因为在有限的机能和简单的算法下，规律始终是容易被发现的（参考第一节的打地鼠）。假如没有玩家动作影响，规律性的掉宝会让玩家非常容易就总结出形如『第二个箱子不打则第五个箱子必出 +100% 生命大血包』的结论，这会极大缩短游戏寿命。而将玩家动作引入后，即使是同一个玩家玩同一个游戏，两次行动也往往并不一致，于是相同游戏进展也就可能掉出各种不同的宝物了。另外，因为玩家并不清楚哪些动作被埋入了影响因子，因此也很难一开始就针对性的调整动作来尝试『探宝』。

在引入玩家动作影响因素以后，什么时候规律才能被发现呢？一是某位玩家熟练到全套过关动作几乎一致时，他才容易发现掉宝似乎也表现出了某种规律性，从而开始探索对掉宝率的控制。这大概就是上面乱步表的由来。另一种是在游戏起始阶段，玩家的行为并不复杂，正好某个掉率也设置较高容易被随机到时，大量玩家的集体行为容易让规律暴露出来。一个第二关开头的水果盘砍出 +2 生命宝物的古老秘籍大概就是这么来的。

而随着硬件性能的不断提升，这种要依靠玩家行为来产生游戏不确定性的情况越来越少了。该方法毕竟是把双刃剑，在可以不用的时候就不必使用了。现在使用任何语言，都有足够多现成的算法可用，并且硬件性能也足以支撑大量的计算了。唯一还需要讲究的大概就是种子值了。

种子对齐

种子和密码正好相反，密码要求前后不变以供核对，而种子则最好每次都不同，因为相同的种子必然产生相同的『随机』序列。如果种子是预先定义好的固定值，服务器每次重启后跑出来的都是相同的序列，开出一样的奖，显然是不合适的。

相同的种子必然产生相同的序列。

发现什么了么？

这意味着，假如你知道某个随机算法的种子，你就拥有了预测能力，精确地知道每一次开奖的结果，就可以批量地安全地赢走电子赌博网站里所有的奖金。甚至就算你不知道种子，发现每次是相同的序列后，也会拿个纸笔记下来吧。在这层意义上，种子值和密码又有了相通之处——不能为人所知。

好办，只要每次种子值都不一样连程序作者自己都不知道不就行了？

——不是这样的。

前文提到最常用的随机种子是时间戳。可是你服务器总要维护重启吧，甚至可能还有自动重启。假如你在凌晨 3:05 重启，直到 3:15 重新开始赌博抽奖。我就知道你这台服务器的赌博程序一定是在 3:05-3:15 之间启动的。假如你真的使用了时间戳作为种子，也一定是在这 10 分种里取的。10 分种，600 秒， 60 万毫秒。大不了把这 60 万个时间全部作为种子挨个跑一遍看哪个能对上你重启后出产的随机序列就好了。能对上的那个序列，对应的时间戳就是你的种子。然后就是原本计划的那样，安全批量地赢走网站里的所有奖金。

好吧，不用时间戳了，使用 CPU 温度吧。同样也不安全，实际运行的机房计算机的 CPU 温度，我们就算它可能是 50℃ ~ 90℃ 吧，传感器温度有限，就算三位小数，那也就是四万种可能情况而已，挨个跑一遍就好了。奖金就到手了。

要知道，计算机不依赖第三方，内部可以提供的变化数据其实就那么几种，而随机算法也只有那么几种。圈定了一个大致的范围以后，『大不了全跑一遍』来反推种子值，其实是非常有效的。相同的随机算法，相同的种子，必然产生相同的序列，于是你就获得了神的预言能力。

那么假如使用外部数据呢，比如前文提到的 random.org。也可以通过 DNS 解析到假网站，提供自己预先准备好的『毒种子』进行攻击。尽管这个方法在 random.org 启用了 SSL 证书以后变得麻烦一些了，但还有更简单的攻击办法，就是让服务器无法访问该网站，直接让你拿不到网站提供的随机种子。

网站总是要经营的，如果服务器一直无法正常运作，损失不比奖金被赢走小。既然种子对齐的目的是赢走奖金，那么当破解难度大到一定程度时，各种攻击勒索就变成收益更高的方式了。

话题似乎跑远了，但其实本文讨论的核心是『计算机随机，够用就好』。当破解的难度大于勒索的成本，基本也就说明在随机算法这一层面，确实够用了。

感觉的随机

『够用』往往还有另一层意思。

我们还是从掉宝率开始，假如一样极品宝物，比如屠龙宝刀 ~~点击就送~~ 在游戏内的掉率为 1%，这意味着大约杀 100 次 boss 会掉一把。作为一个通过反复击杀 boss 获取的装备，掉率 1% 本就是定位于每个人都能获取的高级装备。只要统计一下整个网游的怪物击杀量，就知道那是多么大一个天文数字.如果真要定位为全服稀有，那么掉率必然是几乎接近于零的。

既然是普及型稀有装备，假如一个玩家每天可以杀 boss 一次，那么大约 100 天期望时间也就是三个月左右会掉一把，这也比较符合网游的更新周期。假如有 10 万人玩游戏，那么平均每天大约有 1000 人会获得该武器，通过游戏社区也会刺激其它玩家的游戏动力。随着游戏进程玩家的装备变好，击杀 boss 的速度越来越快，在版本的最后阶段变成例行公事一般，也可以满足游戏运营方对上线率存留率方面的要求。

如果只计算粗放数据，以上一切看起来都很美好。但事实是：

大约有 10,0000 * (1-1%)¹⁰⁰ = 36603 名玩家在三个月以后依然没有获得宝刀；
大约有 10,0000 * (1-1%)¹⁵⁰ = 22145 名玩家在五个月以后依然没有获得宝刀；
大约有 10,0000 * (1-1%)²⁴⁰ = 8963 名玩家在八个月以后依然没有获得宝刀；
大约有 10,0000 * (1-1%)³⁰⁰ = 4904 名玩家在十个月以后依然没有获得宝刀；
大约有 10,0000 * (1-1%)³⁶⁵ = 2552 名玩家在一整年以后依然没有获得宝刀；

对于这几千名玩家而言，怀疑游戏开发商虚假承诺数据做假，完全合情合理。在没有附加条件的 1% 随机掉率下，第一天拿到宝物的就有 1000 名玩家，而运气不好刷一整年都不出的有 2552 名玩家。如果我们考虑得更实际一点，不是每个人都天天刷游戏，实际都是新版本刚开火热一点，后面就是有时间上线没时间算了。那我们假设第一周七天天天刷，第一个月每周刷三次，之后丧失新鲜感失望情绪蔓延，每周只上线一次。则：

大约有 10,0000 * (1- 99%⁷) = 6793 名玩家在第一周拥有了宝刀，一人多刀没用只算一把，每百人有 6.7 把。
大约有 10,0000 * (1- 99%¹⁶) = 14854 名玩家在第一个月拥有了宝刀，每百人里有 14.8 把宝刀，三周涨了 8.1。
大约有 10,0000 * (1- 99%²⁴) = 21432 名玩家在三个月内有了宝刀，每百人里有 21.4 把宝刀，两月涨了 6.6。
大约有 10,0000 * (1- 99%⁶⁴) = 47440 名玩家在一年内有了宝刀，每百人里有 47.4 把宝刀，九月涨了 28.0。

总比例造成未获得者的不快感蔓延，由于击杀频率的减少也导致存量增长下降。游戏根本撑不到一年。

无标题

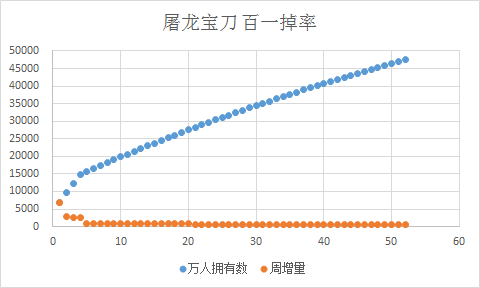
假如我们可以付费买 boss 复活再次击杀获得额外一次掉宝机会——就是花钱开宝箱，则需要 chance = 1146 才能使得 10,0000 * (1-1%)^chance < 1，也就是说运气最差的哥们需要开一千多个箱才能获得这个 1% 几率的宝物。对他而言，这根本就是千分之一的几率。

不患寡而患不均。不加限制条件的纯随机，对那些一次就出的幸运儿很不错，但整体而言其实给玩家的体验并不怎么好。如果有 10% 的几率，玩家可以容忍 20 次甚至 30 次不出，但如果 1% 的几率，能容忍 200 次的都是凤毛麟角。而前者 20 次不出的几率是 12.15%，后者 200 次不出的几率为 13.40%。越是低的掉率，无限制纯随机给玩家的体验就更不好。究其原因，在于人的感觉与概率的实际表现之间存在差异。人人都不觉得自己是最差的那个倒霉蛋，但总有人会填上这个位置。

有两种截然不同的办法去解决这个问题。

一种是尽量去掉这个位置，比如『积累胜率』。当玩家在一次抽奖不中后，略微提升下一次的中奖几率，如若继续不中，则继续提升，直到 100% 必中为止。例如初始 1% 每次提升 1%，那么再倒霉的人在第 100 次开奖时，面对 100% 的中奖几率也该中了。这样的 100 次才中的倒霉蛋，每十万人里大概会有 9.33×10 ^-38 人…… 嗯，十万人中最倒霉的倒霉蛋大约也会在第 45-50 次开奖时得到顶级装备，到不了 100 次。魔兽世界里 “幸运币” 的积累机制就是这么做的。

另一种是分割并加大随机性，让这个倒霉蛋的位置被切分到几乎不可感知。暗黑破坏神 3 里的装备随机属性和随机掉落机制是这种方法的例子之一。对于暗黑3而言，一个人物身上有 13 件装备位置，每个位置都有十几种可能的掉落，但最合适的只有一种。而对于每一件特定装备，又是在十几种不同的属性列表中随机获得四到六种属性，每种属性又是在既定的数值上下限区间随机确定某个值。同时对于一个玩家而言，正常游戏在一小时内即可获得十来二十甚至更多的装备。

尽管绝大部分装备都免不了被嫌弃，但通过这种多装备+多掉落+极大随机的模式，成功地把倒霉蛋的感觉切分到几乎不可感知了。玩家依然可以在论坛上看见别人的极品装备，但对于自己而言，身上也往往会有几件装备是过得去，勉强能让自己满意的，这已经能极大抚慰倒霉蛋们的感受了。

所以有时候，我们反而需要减少一定程度的随机性，使得它感觉起来更随机。

『We’re making it less random to make it feel more random.』

英文那句不是我说的，是乔布斯说的。

在一个既定音乐列表随机播放时，如果是不加限制的随机，经常会出现同一首曲目连续播放两次甚至更多次的情形。这事实上是很正常的事情，如果每次切歌都是从同一个长度为 n 的列表里选取一首，就意味着每次都有 1/n 的几率选到和上一首相同的歌，于是就重复播放了。直接从播放清单移除听过的歌曲可以解决问题，但就和打乱列表的顺序播放没什么区别了。

根据一些访谈所述，苹果 iPod 的随机播放程序是将不同歌手、不同曲风交错播放，让使用者感觉到每一首歌之间毫无关联，相当的“随机”。

所以你看，科学计算需要的随机，和游戏需要的随机，和播放器需要的随机，和自然界的随机，其实都各有不同。

算法服务于目的。