PT 站中的做种公式(魔力值计算)分析
PT 站大多使用了 nexusPHP 的方案,因此其 Seeding Bonus,通常称为魔力点数,基本也使用了相同的公式进行计算:
\begin{align*}
&A = \sum_i\left( 1-10^{ -\frac{T_i}{T_0} } \right) \cdot S_i \cdot \left( 1+\sqrt2 \cdot 10^{ -\frac{N_i-1}{N_0-1} } \right) \\
&B = B_0 \cdot \frac{2}{\pi}arctan\left( \frac{A}{L} \right) \\
\end{align*}
其中:
- 积分每小时计算并发放一次,后文不再赘述。
- $S_i$ 为第 i 个种子的大小,单位是 GB
- $T_i$ 为第 i 个种子发布起到现在经过的时间,单位为周,$T_0$ 为参数,$T_0 = 4$
- $N_i$ 为第 i 个种子当前的做种人数,$N_0$ 为参数,$N_0 = 7$
- $L$ 为参数,$L = 300$,$B_0$ 为参数,$B_0 = 50$,不同站点有时会在 $B_0$ 和 $L$ 上有所调整。
- $B$ 为每小时用户获得的点数,由于 $arctan$ 函数值有上限,因此 $B$ 恒小于 $B_0$
可以看到,对于 A,实质上是对每个种子的体积进行了加权求和,两个系数分别与时间和做种人数有关,实质上还是某种『有效做种体积』。因此先分析第二段公式,使用 Geogebra 绘制函数 $\frac{2}{\pi} \cdot arctan\left( \frac{A}{L} \right)$ 图像并取若干个样点:
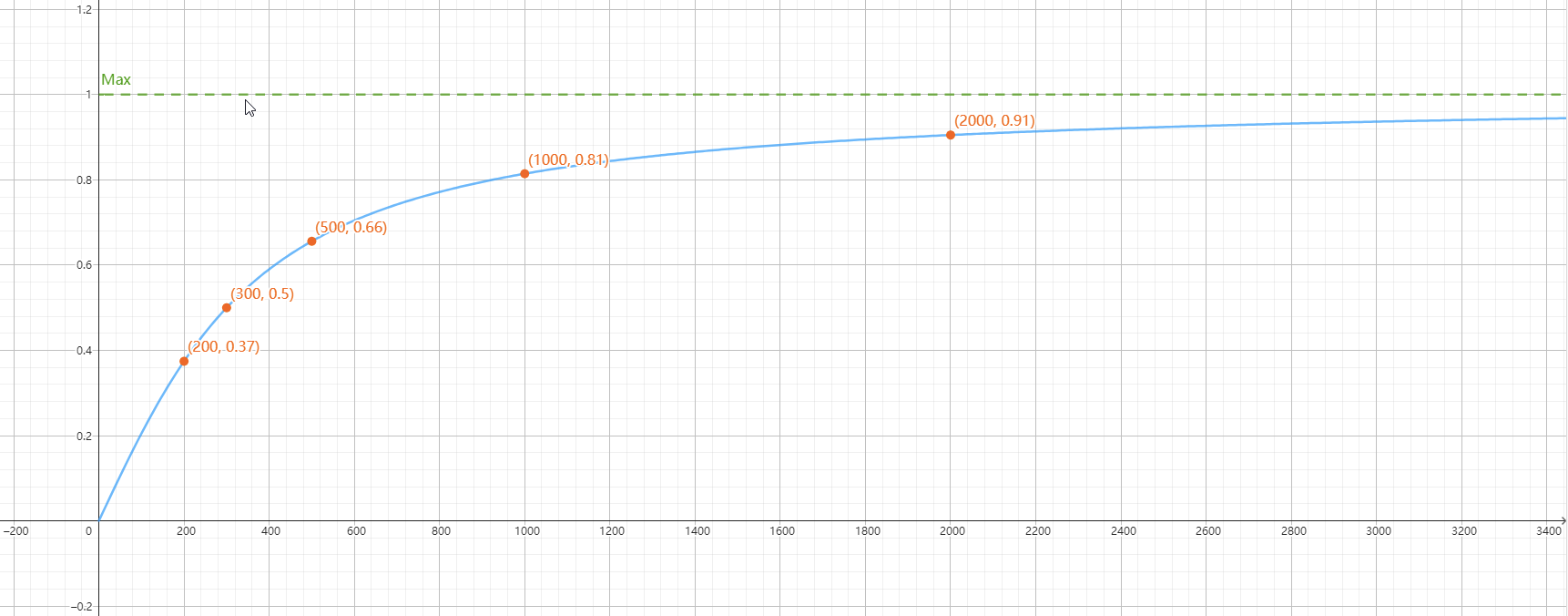
函数图像是个有上限、增幅递减的增函数,在有效做种体积为 200GB 时,可以得到 $0.37B_0$ 的魔力值,在 1000GB 时为 $0.81B_0$。以下列举一些计算结果:
| 加权体积 | 上限比 | 加权体积 | 上限比 | 加权体积 | 上限比 |
|---|---|---|---|---|---|
| 10 GB | 0.0212 $B_0$ | 1 TB | 0.8186 $B_0$ | 15 TB | 0.9876 $B_0$ |
| 25 GB | 0.0529 $B_0$ | 1.5 TB | 0.8772 $B_0$ | 20 TB | 0.9907 $B_0$ |
| 50 GB | 0.1051 $B_0$ | 2 TB | 0.9074 $B_0$ | 25 TB | 0.9925 $B_0$ |
| 75 GB | 0.1560 $B_0$ | 2.5 TB | 0.9257 $B_0$ | 30 TB | 0.9938 $B_0$ |
| 100 GB | 0.2048 $B_0$ | 3 TB | 0.9380 $B_0$ | 35 TB | 0.9947 $B_0$ |
| 200 GB | 0.3743 $B_0$ | 3.5 TB | 0.9468 $B_0$ | 40 TB | 0.9953 $B_0$ |
| 300 GB | 0.5 $B_0$ | 4 TB | 0.9535 $B_0$ | 45 TB | 0.9959 $B_0$ |
| 400 GB | 0.5903 $B_0$ | 4.5 TB | 0.9586 $B_0$ | 50 TB | 0.9963 $B_0$ |
| 500 GB | 0.6560 $B_0$ | 5 TB | 0.9627 $B_0$ | 55 TB | 0.9966 $B_0$ |
| 600 GB | 0.7048 $B_0$ | 6 TB | 0.9689 $B_0$ | 60 TB | 0.9969 $B_0$ |
| 700 GB | 0.7422 $B_0$ | 7 TB | 0.9734 $B_0$ | 70 TB | 0.9973 $B_0$ |
| 800 GB | 0.7716 $B_0$ | 8 TB | 0.9767 $B_0$ | 80 TB | 0.9977 $B_0$ |
| 900 GB | 0.7952 $B_0$ | 9 TB | 0.9793 $B_0$ | 90 TB | 0.9979 $B_0$ |
| 1000 GB | 0.8145 $B_0$ | 10 TB | 0.9814 $B_0$ | 100 TB | 0.9981 $B_0$ |
如果要达到特定的目标上限比,几个档位如下:
| 上限比 | 加权体积 | 上限比 | 加权体积 | 上限比 | 加权体积 |
|---|---|---|---|---|---|
| 0.1 $B_0$ | 48 GB | 0.91 $B_0$ | 2108 GB (2.06 TB) | 0.991 $B_0$ | 21220 GB (20.72 TB) |
| 0.2 $B_0$ | 98 GB | 0.92 $B_0$ | 2375 GB (2.32 TB) | 0.992 $B_0$ | 23872 GB (23.31 TB) |
| 0.3 $B_0$ | 153 GB | 0.93 $B_0$ | 2718 GB (2.65 TB) | 0.993 $B_0$ | 27283 GB (26.64 TB) |
| 0.4 $B_0$ | 218 GB | 0.94 $B_0$ | 3174 GB (3.10 TB) | 0.994 $B_0$ | 31831 GB (31.08 TB) |
| 0.5 $B_0$ | 300 GB | 0.95 $B_0$ | 3812 GB (3.72 TB) | 0.995 $B_0$ | 38197 GB (37.30 TB) |
| 0.6 $B_0$ | 413 GB | 0.96 $B_0$ | 4769 GB (4.66 TB) | 0.996 $B_0$ | 47746 GB (46.63 TB) |
| 0.7 $B_0$ | 589 GB | 0.97 $B_0$ | 6362 GB (6.21 TB) | 0.997 $B_0$ | 63662 GB (62.17 TB) |
| 0.8 $B_0$ | 924 GB | 0.98 $B_0$ | 9547 GB (9.32 TB) | 0.998 $B_0$ | 95493 GB (93.25 TB) |
| 0.9 $B_0$ | 1895 GB | 0.99 $B_0$ | 19098 GB (18.65 TB) | 0.999 $B_0$ | 190986 GB (186.51 TB) |
200 GB 以下大致可视为线性增长,2 TB 时可以达到 90% 上限分数,更高的分值需要极大的硬盘空间,逐渐不甚合理了。$L$ 参数的变化会等比例地影响上表中的加权体积数值。
下面来研究两个系数的影响,这两个系数实现了『实际做种体积』$\rightarrow$『有效做种体积』之间的换算。首先是时间系数,$f(T_i) = \left(1-10^{ -\frac{T_i}{T_0}}\right)$,由于 nexusPHP 本身对该分值是基于小数的,且『周』的展示不甚直观,这里直接改用『天』作为单位,换算 $T_0 = 28$,其图像为:
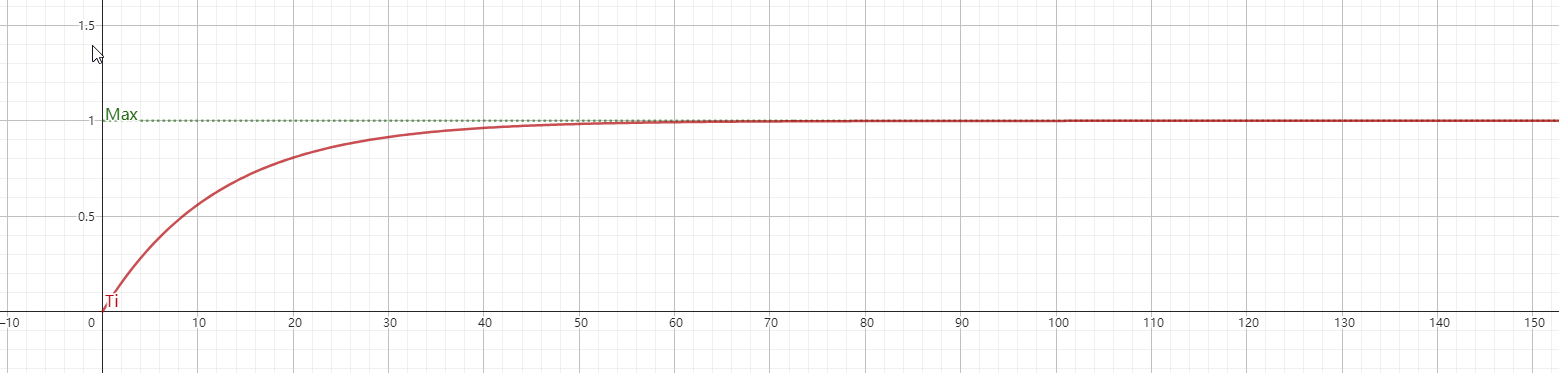
显然这也是和 arctan 一样的有上限、增幅递减的增函数,但增幅比 arctan 要大得多,靠近上限十分容易,也就是说到达 0.999 或更高值是个可行的目标。以下列举一些计算结果:
| 时间 | 系数 | 时间 | 系数 | 时间 | 系数 |
|---|---|---|---|---|---|
| 1 小时 | 0.0034 | 2 天 | 0.1517 | 9 天 | 0.5229 |
| 2 小时 | 0.0068 | 3 天 | 0.2186 | 15 天 | 0.7087 |
| 3 小时 | 0.0102 | 4 天 | 0.2803 | 28 天(4 周) | 0.9 |
| 6 小时 | 0.0203 | 5 天 | 0.3371 | 56 天(8 周) | 0.99 |
| 12 小时 | 0.0403 | 6 天 | 0.3895 | 84 天(12 周) | 0.999 |
| 24 小时 | 0.0789 | 7 天 | 0.4377 | 112 天(16 周) | 0.9999 |
因为是 10 的幂运算,计算分段明显。每 28 天小数点后多一位 9,在寻找 free 种子攒积分时,选时间大于三个月 (>0.999) 的就行,『实际做种体积』与『有效做种体积』几乎一致。
最后是做种人数系数,$f(N_i) = \left(1+\sqrt2 \cdot 10^{ -\frac{N_i-1}{N_0-1}}\right)$,在其定义域内这是个有上下限的减函数,其图像为:
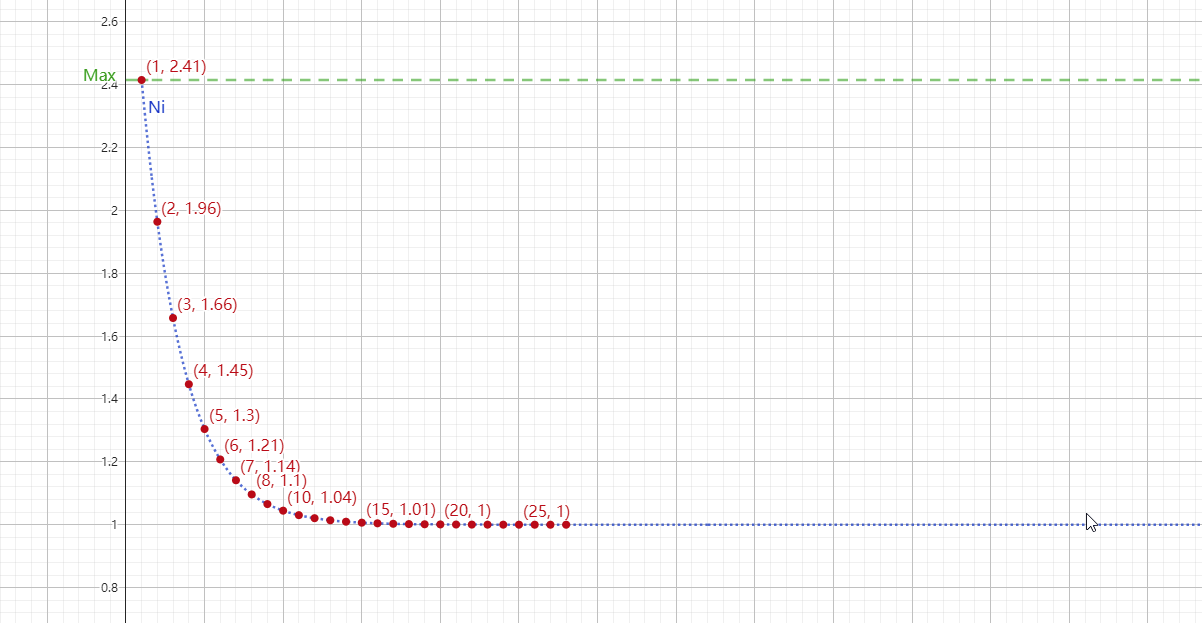
与前两个系数不同,$N_i$ 做种人数只能取正整数,因此其图像是离散的。以下列举一些计算结果:
| 做种人数 | 系数 | 做种人数 | 系数 | 做种人数 | 系数 |
|---|---|---|---|---|---|
| 1 | 2.4142 | 6 | 1.2076 | 12 | 1.0208 |
| 2 | 1.9635 | 7 | 1.1414 | 14 | 1.0100 |
| 3 | 1.6564 | 8 | 1.0963 | 20 | 1.0010 |
| 4 | 1.4472 | 9 | 1.0656 | 26 | 1.0001 |
| 5 | 1.3047 | 10 | 1.0447 | 28 | 1.0000 |
可以看到,只有 8 人以下的种子才有可能达到 >1.1 的系数,而 20 人以上的种子,该系数的增益已经完全可以忽略了。由于做种人数是不可控的,因此可以简单划为两类,20 人以下有加成, 20 人以上无。又因为人数会变动,因此若要从这个系数上获得稳定收益,必须考虑 $N_i<8$ 的种子,以容许一些浮动范围。
通过以上两个系数的分析,可以得到一个结论,我称为『三八原则』:
三八原则:在 PT 站做种赚取积分时,选择时间大于三个月,做种人数小于 8 人的种子。
原则展开如下:
- 做种人数足够少,可以使实际 1GB 的硬盘空间达成 2.4GB 的做种效果,但条件苛刻。
- 但再多的做种人数也不过是系数为 1,没有奖励,但不会有折损。
- 三个月以前的种子,做种效果几乎 1:1 且容易达成。而一个月以内则折损可观,不是没得选尽量避免保新种。
- 积分有上限,有效做种体积 1-2 TB 已经可以达到 80%-90% 的上限了。再增长 10% 到 99% 则需要近 20TB 有效保种,即使都是长寿孤种也需要 8TB,意义不大。
- 形势所迫必须新种,则放置一周有 44% 的有效做种体积,准备 4TB 硬盘也就够了。
- 孤种才有奖励,新种只有折损。
这样可以最大化体积系数,从而用相同的硬盘空间获取更大的做种收益。当然,既然是赚取积分,肯定是要选择 free 种子。种子时间可以挑选,但做种人数加成八成是不必指望了。
其它一些 Bonus:
各站点会根据自己的实际调整参数,或添加其它的奖励机制,例如:
每个种子 0.7 基本分,最多 14 个。
该数值上限 9.8,是直接作为基础值的,因此该站的积分上限为 $9.8+B_0$。这个条件几乎不存在代价,保种 1-2 TB 通常来说都会超过 14 个种子。
用户等级奖励,每升一级 1% 的比例奖励。
这个奖励是在基础值之外的奖励,计算公式为 $(1+1\%\times Level) * (9.8+B_0)$
用户等级奖励其实存在很大的隐性的代价。PT 站往往要求上传量远大于下载量才能升级,而 1% 的奖励却聊胜于无。这就像在银行存一百万拿 2% 的利息,银行要求你再存一千万升 VIP,而 VIP 的待遇仅仅是利息多 1%,并不是 $2\%\rightarrow 3\%$ 的 1%,而是 $2\%\rightarrow 2.02\%$ 的 1%。如果上传本有余裕,自然升级也就罢了,刻意去为 1% 奖励而花大力气冲没什么意义。
为官方种子做种的额外奖励,上限为 25%。
百分比类型奖励都是平行的,也就是 $(1+1\%\times Level + 25\%) * (9.8+B_0)$。
注:该站点程序有 bug,多个官种奖励叠加反而会导致总 bonus 下降,因此只保一个 +25% 官种即可。每 100 个种子做种 24 小时以上开始 5% 的比例奖励,无上限,每个种子需要大于 5MB。
$$(1+1\%\times Level + 25\% + \mathop{SeedsQuantity}\limits_{\substack{seedsize>5\text{MB} \\ seedinghour>24}} / 100 \times 5\%) * (9.8+B_0)$$
该规则鼓励大量小体积种子做种,理论上来说,以 2TB 的目标计算,若全部靠 5MB 的种子达成,至多可以使用 40 万个种子,单这项 bonus 就能达到 $200B_0$,这是一个巨大的增益。客观上受限于种子总量有限及大小各异,不可能达到这个数量,但成为一个万种大佬还是有可能的。此时的 bonus 为 $$(1+25\%+\frac{10000}{100}*5\%) \times (9.8+0.9\times B_0) = 6.25 \times (9.8+0.9\times B_0)$$ 若 $B_0=50$,则值为 $342.5$。在该规则下,保种策略是尽量地将大种子更替为小种子,在总量有限而不变的情况下,提升种子数量。
但是我们需要进一步讨论。更替小种虽有额外收益但通常也会产生额外的下载流量,需要靠魔力值兑换上传量来冲抵。一个种子的小时增益为 $5\% / 100 \times (9.8 + 0.9B_0) = 0.0274$,每天可以通过魔力值兑换的上传流量为 $0.0274 \times 24 \; / \; 425 \times 1024 = 1.5844$ MB,一个 5MB 的种子在 3.15 天回本,因为是独立计算,一百个 5MB 的种子也是 3.15 天回本。回本时间不受种子数量的影响,但与种子体积成正比,当种子体积到 50MB 时回本时间就超过一个月了。
另一需要考虑的软性限制是 PT 与站点服务器的通讯。当做种数量足够多时,PT 客户端的 tracker update 操作变得十分频繁,甚至变相成为一种对服务器的 DOS 攻击。这也是热门大站往往 tracker update interval 很长的原因。大量种子对保种用户本身也是存在风险的,对同一地址的短时间频繁请求,在客户端到服务器的整条网络传输路径上的任何一个环节都有可能触发限制。服务器收不到 update 信息,用户就反而无法获得积分。
使用 $250\times B_0$ 的价格购买 5% 比例的奖励徽章,可购买多个。
同样是某种需要考虑投入产出的增益。该站点没有其它基础值奖励,以每小时 $0.9B_0$ 计算,购买后的增益为 $0.045B_0$,回本时间为 $250B_0 /0.045B_0 / 24 = 231.49$ 天。该站 50G 上传量为 $50B_0$,一个徽章相当于 250 GB 的上传量。从无穷长远来看,一切本金不会湮灭且无通胀环境下的投入都是值得的,算来第 232 天开始可就是净收益了。但是在合理的生命周期内,这个投入产出比是十分低的。因此这个徽章是一个『炫耀』的物品,而不是一个『赚钱』的物品。
PT 站的生命周期是客观存在的,对于用户方,如果生活中发生了某些变化,帐号有时就冷落消失了。对于站点方,也有可能因为各种原因关闭跑路。长周期的收益更多只是在纸面上的。
相聚离开都有时候,没有什么会永垂不朽。
后宫加成,每个下线 5%。
这个奖励的 ROI 计算更为复杂,暂不清楚是否有复利加成,即我后宫的后宫是不是我的后宫。单从实践经验来看,$50B_0$ 兑换邀请和赠与新人 $62.5B_0$ 启动资金,换得的是下线的 5% 增益。如果下线足够给力,则可以得到和徽章奖励一致的 $0.045B_0$。回本周期为 105 天。考虑到下线需要积累一段时间才能达到 $0.9B_0$,实际周期在 150 天左右。比起奖章仍合算一些。如果不提供启动资金,回本周期为 47 天,但新人启动时间会长不少,相当于额外再增加一个 0-50G 的启动时间。
如果考虑风险因素,ROI 就不好说了。下线的行为是不可控的,且会影响到自己的账号。$112.5B_0$ 的本金浪费是一方面,其它权利影响是则另一方面。除非有站点相关数据作为支撑,否则这些风险很难量化。
从奖池中抽道具,部分道具增加 10% 基础魔力值奖励,每次抽取动作消耗 $2.5B_0$。
从 n 个道具中抽取特定的 k 个道具,假设无重复时,全部抽齐的期望次数为 $\frac{k(n+1)}{k+1}$,则成本为 $\frac{k(n+1)}{k+1} \times 2.5B_0$,收益为 $k \times 10\% \times 0.9B_0$,回本周期为 $1.1574 \cdot \frac{n+1}{k+1}$ 天,取决于奖池 n 和 k 的比例。事实上哪怕是 1/100 的比例,也比上一条后宫加成更合算。
进一步考虑,第一个道具在抽出后开始生效,其成本为 $\frac{n+1}{k+1}\times 2.5B_0$,收益为 $10\% \times 0.9B_0$,回本周期同样为 $1.1574 \cdot \frac{n+1}{k+1}$ 天。也就是说,在整个过程中,每个道具的奖励比例一致,则回本周期也都是一致的。
当有重复时,情况则有不同,第一个的期望成本为 $n/k\times 2.5B_0$,回本周期为 $1.1574 n/k$ 天。所有奖品抽到的期望次数为 $n\cdot H_k$,其中 $H_k=\sum_{i=1}^n\frac{1}{i}$ 为调和级数。越往后面,即使奖励相同,但抽取成本变大也会导致回本周期变长。最后一个的成本是 $n\times 2.5B_0$,回本周期对应为 $1.1574 n$ 天。
如果除 k 外的其它道具也有一定的奖励,或者总数 n 难以计算,则 ROI 的计算只能通过少量抽样下的贝叶斯推断来进行了。
上传流量的奖励,每 1GB 上传流量奖励 0.1 魔力值。
PT 站本身上传量就是货币,这个其实属于某种重复奖励,且没有可优化或者可选择的余地。不讨论。
末尾一些啰嗦:
$f(A) = B_0 \cdot \frac{2}{\pi} \cdot arctan\left( \frac{A}{L} \right)$ 的导数为 $f^{'}(A) = \frac{2B_0}{\pi L} \cdot \frac{1}{1+\left( \frac{A}{L} \right)^2}$,为 $\frac{1}{1+x^2}$ 的缩放。当前每增加 1GB 的有效做种体积对应多少魔力值增量,可以通过导数来计算。
通过计算 $Total\_Bonus = N_i \cdot \left(\sqrt2 \cdot 10^{ -\frac{N_i-1}{N_0-1}}\right)$ 发现,在 3 人及以下做种时,PT 站额外奖励了更多的体积系数分到所有的人,而人数更多时 Bonus 总增益开始下降,奖励总量反而逐渐减少。算法并非是将固定的 Bonus 分发给所有人,而确实是针对孤种的单独加成: