素数算法,外加点糖
质数,也叫素数,是对 Prime Number 的不同翻译。素数的叫法大概率来自日语,素在日语里引申出了根本,源头以及不可再分割的意思,这一点古汉语里是没有的。因此诞生出了一大批和制词汇,比如元素,素材,要素等等。而 Prime Number 正好符合这个特性,叫素数再合适不过了。现代汉语由于引入了上面这些和制词汇,所以素也开始有了上述意思。至于港台地区保留了这个叫法也是因为延袭了民国时期的翻译习惯,没有做变更而已。
《为什么叫素数》 来源:Spenser Sheng
链接:https://www.zhihu.com/question/22456389/answer/967574484
至此,质数这个名词就在中国成了官方认可的科学术语,并一直没用至今。但是,素数这个说法并没有因此退出历史舞台。同时代的秀多著作,还是用了这个名词,比如华罗庚先生于 1940 年出版的《堆垒素数论》等。这直接影响了后来更多数学家在著书立说时没用素数这个名词(可能因为要考虑与他人表述的统一性),如陈景润研究“哥德巴赫猜想”也是讲素数。……在中小学教材上,目前是统一使用质数这个名词,但是标明了“质数,又叫素数”《梳理源流,叩问本质——对质数、合数名词的考证与思考》顾志能 https://www.doc88.com/p-1478574668277.html
如何计算 N 以内的素数,或者判断 p 为素数,在编程领域是孪生的两个问题,也是很多编程语言的入门题目。这个题目优点在于有相当多的解法和优化空间,尤其适合用来练习算法和程序优化。这里我们就来逐步优化一个素数计算程序。
基础实现
我们从最简单的开始,先写一个函数 isPrime(n) 判断 n 是否为素数,这个判断函数严格按素数的定义实现:
除了 1 和 n 之外,没有其他整数能整除 n
也就是说,将 2 ~ n-1 之间的每个整数都试一遍,看看是否能整除 n。再用 isPrime(n) 逐个找出 < N 的所有素数。
1 | function isPrime(n) { |
※ 本文演示代码为 JavaScript,方便在浏览器控制台内测试。但考虑到与正文内容保持一致,并未使用 JavaScript 内置的 .map(), .forEach(), .filter() 等遍历函数,而只用普通的 for loop if else 等代码。
简单优化
显然上面的代码是有很多无效的计算的,一些简单的数学知识就可以大幅地优化计算效率:
- 所有的偶数都不是素数,除了 2。
1 | function calcPrimes(n) { |
- 同上,所有 3 的倍数都不是素数,除了 3。因此,我们可以只检查 6k ± 1 的数。
1 | function calcPrimes(n) { |
※ 理论上我们可以继续讨论 5 的倍数,但这会使 for 循环需要处理 30k ± a,且 a 有 1,7,13 等多个值。代码变得复杂,而优化效果一般。过于复杂的代码会让你不幸福。
- 判断素数时,只需要检查到 sqrt(n) 即可。如果 n 有一个大于 sqrt(n) 的因子,必然对应一个小于 sqrt(n) 的因子,则之前的循环中已经判断过了。
1 | function isPrime(n) { |
更多优化
进一步思考 isPrime 函数,我们发现,不必让所有小于 sqrt(n) 的数都试一遍,只需要用之前已经计算出来的素数尝试即可。但我们需要整体调整代码,使 isPrime() 函数可以调用 primes 数组。
1 | function calcPrimes(n) { |
筛法
以上的方法都是用较小的数字去尝试整除 N 以判断 N 是否为素数,这种方法称为试除法。从直观考虑,每个 N 都会被 2,3,5 ... 等数字都除一遍,比如 49 和 77 都会在 2, 3, 5 上各浪费三次计算。如果可以绕过无效除法,只用 7 去尝试 49,而 2,3,5 则不去浪费时间,耗时会大幅会降低。事实上这种方法是存在的,并且非常简单,称为『筛法』。
简单到解释起来只需要两句话:
- 从 2 开始,将所有 2 的倍数都划掉;从 3 开始,将所有 3 的倍数都划掉;从 5 开始,将所有 5 的倍数都划掉;
- 以此类推。
1 | function calcPrimes(n) { |
这个筛法也被称为埃拉托斯特尼筛法,是为了纪念古希腊数学家埃拉托斯特尼而命名的。这个方法看似很简单,实际也确实很简单,是一种朴素的空间换时间方案。算法改除法为乘法,同时避免互质两数相遇,避免了很多无效运算。虽然当 N 非常大时,numboard 数组会占用很多内存,但时间优势更为明显。
※ 由于这个方法如此简单,普通人也能想到,不值得特地冠名。我猜测这个名字只是为了纪念历史名人,不能说明是他最早发明了这个方法。
同样,上述代码也有一些优化空间,比如:
- 划掉倍数时,可以从 j = i*i 开始,因为 2i, 3i ... (i-1)i 在对应的 2, 3 ... i-1(或其因数)那一轮时已经被划掉了。
- 当划到 i > sqrt(N) 时,则剩余未标记数也都是素数。假设有任意合数 m 满足 sqrt(N) < m < N,则 m 的素因数 p1,p2 ... 中最小的一个 p 也必然小于 sqrt(N)。而我们已经找到所有小时 sqrt(N) 的素数,并划掉其倍数了,所以找到 p 时必定已经划掉 m。
1 | function calcPrimes(n) { |
在算法进入筛法层次后,isPrime() 函数与 calcPrimes() 函数的功能区别也就不再明显。为了判断 N 是否为素数,需要至少计算到 sqrt(N) 的素数,而上文又证明剩余的未标记数也都是素数。差别只是最后判断一下 N 是否在 primes 数组中而已。
另外,在埃氏筛法中,6k ± 1 等手段不再有优化作用。构造一个『只有奇数的筛盘』是可以的,但后续的划除操作需要大量的脚标奇偶运算,反而会增加计算量。
位运算
在埃氏筛法中,内存占用是一个问题,尤其在筛法本身就是为了计算大 N 而生的。在实际应用中,有时也需要在有限的内存空间内尽量优化。注意到 numboard 数组只是用来标记是否为素数,只需要 0,1 两个状态,因此可以用位运算来减少内存占用。这使得内存的占用降为原来的 1/8。但此时算法的实现与编程语言也开始耦合,不是每种编程语言都支持直接的位运算,例如 JavaScript 的位运算就只是某种『模拟』,效率并不高。Javascript 也不支持直接修改某个 bit 位,而要经过多次字节操作来实现。尽管如此,我们仍可以编写一个 setBitFalse() 函数来模拟这个操作:
1 | function setBitFalse(arr, i) { |
代码解释:
- JavaScript 里数值默认 32 位,通过 i >> 5 相当于 i/32 取整,可以得到对应的数组下标,即具体操作哪个元素。
- i & 31 将 i 与 31 (00001111) 进行按位与操作,相当于对 32 取余,得到具体操作该元素的第几个 bit 位。
- 1 << (i & 31) 将 1 左移 i & 31 位,得到一个只有第 i & 31 位为 1 的数,即只有指定 bit 位是 1 其它都是 0 的掩码。
- ~( ... ) 按位取反以后就得到了 1111....0...111 的反掩码,只有指定 bit 位为 0。
- &= 是按位与且赋值,将数组指定元素与反掩码进行按位与运算,其它位与 1 后值不变,指定 bit 位则变为 0。目标达成。
然后,我们需要写一个 isBitTrue() 函数来判断某个位是否为 1:
1 | function isBitTrue(arr, i) { |
类似地,函数计算数组下标和 bit 位置,生成一个只有指定 bit 位是 1 的掩码,将其与数组元素进行按位与操作。因为按位与操作遇 0 必 0,所以其它位都会被掩码数值置为 0。如果结果不为 0,则说明数组元素与掩码在该 bit 位上都是 1。
最后,我们还需要写一个 bitsToNums() 函数,将位运算后的结果数组转换为素数数组:
1 | function bitsToNums(arr,n) { |
将几个函数代入原程序中的对应位置,我们可以得到一个位运算版本的埃拉托斯特尼筛选算法:
1 | function calcPrimes(n) { |
可以看到,位运算版本的代码更为复杂,原本只是根据下标取数组元素并判断 true/false 的操作,现在需要生成掩码,计算偏移量,转换位数等多次计算。只有在 N 极大,以至于必须减少内存占用的情况下,才需要使用位运算。在一般情况下并不值得作此妥协。
同时,对于 JavaScript / Python / java 等高级语言,位运算的效率并不高。即使实际情况确实拮据,也必须先考虑更换编程语言。比如在 C++ 中,std::bitset 这种数据结构,就特别适合于埃氏筛法结合位运算计算素数表。
分段筛法
说到内存不足,很容易就能想到另一种解决方案:分段筛法。在筛选过程中,我们把素数放进了单独的 primes 数组,而 numboard 数组则只是用来筛除合数。当 primes 找到大小为 p 的素数,就意味着 p*p 之前的 numboard 数据已经没有用了,如果我们能把这部分内存释放掉,就能大幅减少内存占用。
因此从逻辑上讲,当求 N 以内的素数时,我们只需要保留 sqrt(N) 以内的素数,并将整个 N 范围划为若干块,对每一块使用 primes 数组进行筛选。如果不考虑分块本身的内存分配回收时间,单只考虑数值与操作量的话,分段筛法的时间复杂度与原始筛法是相同的。对于每一个被筛选的元素,都会被其每一个独特的素因数筛选一次,无论是在全局 numboard 中,还是在局部 numboard_i 中,都一样。
基于前文的铺垫,似乎分块大小设置为 sqrt(N) 是直觉上合理的方案。但实践中,分块大小更多与内存大小有关。比如 nodejs 的默认内存上限为 2GB,尽管可以通过 --max-old-space-size 参数调整,但在个人电脑环境下再提升其实也并不会有什么质变。只要确保 primes 数组空间的前提下仍有足够的内存,就是合理的块大小。
1 | // JavaScript 数值默认 4Byte,1GB 内存可以存储 2^28 个数值。约 2.68 * 10^8 个。 |
欧拉筛法
在埃氏筛法中,我们注意到,数字 6 会被 2, 3 划掉两次,30 会被 2, 3, 5 划掉三次。所有合数都会被其不同的素因数重复操作若干次,浪费还是有不少。但我们并不能去判断筛盘上某个具体的数是否已经划掉,因为『读取与判断』的时间本身可能比直接划掉时间还长。
进一步用力注意到,筛法的本质是从『验证素数』变成了『排除合数』,而且是有规律的排除合数。考察一个合数 6 = 2 x 3,我们希望在算法中,2 x 3 只发生一次,而不是在 2 与 3 的循环中各发生一次。对于 12 也一样,尽管它有 2 x 2 x 3, 4 x 3, 6 x 2 这三种分解方式,但我们希望只有其中一种发生,其它的被跳过。
仿佛一头雾水但哪里又有一些灵感,这好像是可能的,只要足够聪明合理地安排合数生成,好像可以做到?
事实确实如此。欧拉筛法就是为了解决这个问题而生的。具体操作是这样的:
- 有一个自增的数字 i,从 2 开始。
- 有一个数组 primes,存放已经找到的素数。
- 如果筛板上 i 还没被划掉,则 i 是素数,将其加入 primes 数组。
- 用每一个 i 乘以当前所有 primes 中的素数,得到的数都是合数,在筛板将它们标记为 false 划掉。
- 如果 i 是 primes 中某个素数的倍数,那么 i * p 这个数会被标记 false,但后续直接跳过,进到 i+1 轮。
1 | function calcPrimes(n) { |
在欧拉筛中,我们通过 i * primes[j] 的方式来筛除合数,且当 i 本身为 primes[j] 的倍数时,跳过 i 与后续素数的计算环节。例如:
- 当 i = 4 时,本应划掉 4 * 2 与 4 * 3,但可以跳过 4 * 3,因为它会被后续的 6 * 2 划掉。
- 当 i = 35 时,会先划掉 35 * 5,而 35 * 7 会被跳过,因为它将在 i = 49 时被 5 划掉。
一般来说,如果 i = k * primes[j],则接下来要划掉的 s = i * primes[j+1] = k * primes[j] * primes[j+1] 会在 i' = k * primes[j+1] 轮次时会被 primes[j] 划掉(因为 primes[j] 是 i' 的最小素因子),所以此时可以先跳过。
可以看到,在欧拉筛法中,由于 primes 是从小到大排列的,因此每个合数只在其最小素因数 m 对应的 i = n / m 轮次时,才会被划掉。
在这个算法中,合数的分解是唯一且有序的,因此欧拉筛与埃筛内存占用一样,但算法复杂度优化到了大约 O(n)。——严格来说,因为一些必须的额外判断,实际是 $O(nlog_2log_2n)$。
※ 数学先师的伟业至今仍被人传颂,有一个算法以他的名字命名。纵然身为一个 18 世纪数学家,那个时代还远未出现计算机。
素数的分布
有了高效的素数筛选算法,我们可以开始搜索大范围的素数了。计算 1 亿以内的素数,并每 10 万分为一组,统计每组的数量。可以看到,虽然有波动,但整体是逐渐减少的,并且这个图好像有点眼熟?
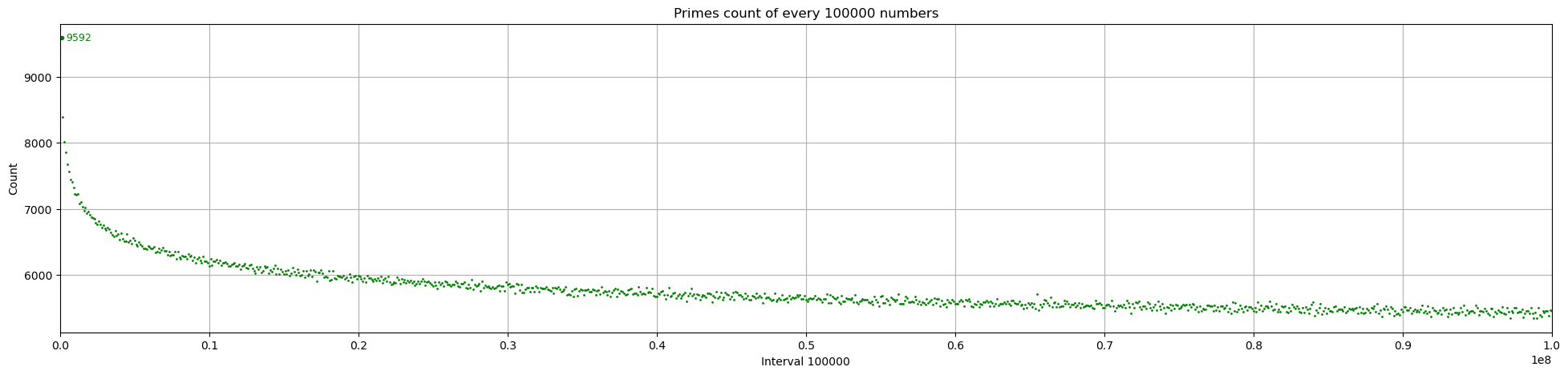
事实上,确实有一个 素数渐近分布定理,大致描述了素数的分布规律:
设不大于 n 的所有素数的个数为 π(n),则 π(n) ≈ n / ln(n)
具体举例来说,当 n = 1 亿时,使用前文的程序计算出素数具体有 5761455 个,而 $n/ln(n)\approx 5428681$,两者比例为 1.061,较为近似。而当 n→∞ 时,值趋近于 1。
另外也可以得到一个推论,在 n 附近随机取一个数字,它是素数的概率是 $P(n)\approx 1/ln(n)$。函数下降不算快,就算 n = 1 亿,概率也有 1/18.42,5.43%。
这个定理已经被证明,但这个值本身只是一个渐近值。也就是说,虽然 $\lim\limits_{x \rightarrow 0}\frac{\pi(n)}{ n / ln(n)} = 1$,但 $\lim\limits_{x \rightarrow 0} [\pi(n) - n / ln(n)]$ 却是越来越大的。从函数图像上而言,两者只是越来越接近于平行,但距离却越来越远。
素数的分布规律是数论的一个重要研究方向。后来数学家又提出了几个更精确的估算公式,这一方向的顶点便是著名的黎曼猜想。
梅森素数与 Lucas-Lehmer 检验。
在了解素数的大致分布,并回顾欧拉筛法以后,我们发现即使是 O(n) 的算法也仍然有很大的局限性。内存限制是最初的现实问题,但也只是所有问题中最简单的一个,更大的限制仍然是来自于算法本身。我们要筛到至少 sqrt(N),才能得到 N 是否为素数的结果。在 N 非常非常大时,O(n) 的算法仍然太慢了。
仔细思考发现,这是因为筛法天然地要求算法结果的素数是连续的,如果跳过某个数,那么后续的合数也可能被认为是素数,整体就会崩盘。那么是否存在『跳过一部分数,快速往更大的素数 N 前进』,以及在不知道小于 sqrt(N) 全部素数的情况下,判断 N 是否为素数的算法呢?
两者都是存在的,并且有多种方法。典型例子是梅森素数和配套的 Lucas-Lehmer 算法。
梅森素数是形如 $2^p - 1$ 的素数,并且简单可以证明,当 $2^p - 1$为素数时,p 也是素数。
当 p 是合数时,令 p = ab,有:
$2^p-1= (2^a)^b - 1 \overset{ x=2^a}{=\!=\!=} (x - 1)\cdot[x^{b-1}+x^{b-2}+\cdots+x+1]$ 为合数。
尽管反过来并不一定成立,当 p 是素数时,$2^p - 1$ 仍可能是合数,比如 2^11 - 1 = 2047 = 23 x 89。但即使如此,梅森素数依然有很多优点,比如:
- 比普通的序列增长得更快,可以跳过很多中间的数,尽快找到更大的素数。
- $2^p - 1$ 中包含素数的比例比全体自然中要高,因此更容易找到素数。
- 否定性验证很容易,只需要验证 p 是否为素数。正向验证难度也比一般的低。
Lucas-Lehmer 算法是验证梅森素数的一种方法。它构造了一个递推公式:
\begin{equation*}
s_i=\begin{cases} 4, & i=0 \\ (s_{i-1}^2-2) \mod (2^p-1), & i>0 \end{cases}
\end{equation*}
则当 $s_{p-2} \equiv 0 \pmod{2^p-1}$ 时,$2^p - 1$ 为素数。其算法复杂度为 $O((log\underset{2}{}n)^2)$。
※ 在大数环境下的计算需要编程语言和专门的数学包支持,代码就不放了
由于梅森素数拥有的诸多优点,目前已知的最大素数都是梅森素数,也有专门的 互联网协作项目 GIMPS 来众算更大的梅森素数。该项目前段时间正好确认了 M(57885161) 是一个新发现的素数。
质性检验
从梅森素数我们得到启发,在合理添加一些额外的限制条件后,素数的出现概率会提高,检验手段也可以针对性设计而变得简单,这对大素数的搜索非常有帮助。
在这个层次上,calcPrimes() 基本就不再是人们的目标,而 isPrime() 则不断地发展,成为专门的『质性测试』算法。这些算法的目标是尽可能快地判断一个数是否为素数,而不是找到所有素数。在这个领域,有很多经典的算法,比如:
Lucas-Lehmer 检验
上文提到的梅森素数检验算法。仅适用于 $2^p - 1$ 形式的素数。
Pépin 检验
验证费马数 $2^{2^n} + 1$ 是否为素数的算法。但由于费马数目前只发现 n=0,1,2,3,4 五个,后面都是合数,甚至有猜想认为 n > 4 时皆为合数。因此 Pépin 检验的应用范围有限。而欧拉和卢卡斯接力证明了费马数的素因数皆可表达为 $k^{2n+2} + 1$,为具体的因数分解也提供了不小的方便。
※ 感觉 Pépin 被费马坑了。
Miller-Rabin 素数测试算法
一个随机性的否定性算法。当测试结果为 false 则一定是合数,测试结果为 true 可能为素数。算法基于费马小定理和二次探测定理,在进行 n 次测试后,错误概率为 $1/4^n$。
费马小定理:如果 p 是一个素数,而 a 是任意不是 p 的倍数的整数,则 $a^{p-1} ≡ 1 (mod\ p)$。这意味着对于任意素数 p,选择一个不是 p 的倍数的整数 a,计算 $a^{p-1}\ \% \ p$,如果不等于 1,则 p 一定不是素数;等于 1,则 p 可能是素数 。
二次探测定理:假设 p 是一个素数,我们可以将 p-1 写为 $2^s * d$ 的形式,其中 d 是奇数。则对于任意整数 a,如果存在整数 x 满足:
- $a^d ≡ 1 (mod\ p)$
- 存在一个 i 满足 0 ≤ i < s,使得 $a^{2^i * d} ≡ -1 (mod\ p)$
以上两个条件之一,则 a 是一个模 p 的非平凡平方根,即 $a^2 ≡ x (mod\ p)$:
假设我们要测试数字 p = 17 是否为素数。
选择不是 p 的倍数的整数 a,假设选择 a = 3。计算 $a^{p-1}\ \%\ p = 3^{16} \% 17 = 1$ 结果等于 1。根据费马小定理,17 可能是素数。
根据二次探测定理,当 p = 17,有 $p-1=16=2^4*1$,因此 s = 4,d = 1。我们需验证任意整数 a,可以满足以下两个条件之一:
- $a^d = a ≡ 1 (mod 17)$
- 存在一个 i 满足 0 ≤ i < 4,使得 $a^{2^i} ≡ -1 (mod 17)$
假若仍然选择 a=3,则 $3 \% 17 =3 \neq 1$,不满足条件一,继续检验条件二:
- $i=0, 3^{2^0}\ \% 17 = 3$
- $i=1, 3^{2^1}\ \% 17 = 9$
- $i=2, 3^{2^2}\ \% 17 = 13$
- $i=3, 3^{2^3}\ \% 17 = 16 = -1$,满足条件。因此 17 可能是素数。
继续类似地进行多轮测试,如果任意一轮验证失败,则 p 一定是合数,反之随着验证轮次增加,p 为素数的可能性便越来越大。
AKS 类质性测试
一个确定性的质性测试算法,复杂度为 $O(log^{6+\epsilon}n)$。AKS 是第一个被发表的一般的、多项式的、确定性的和无依赖的素数判定算法。算法基于一个简单定理:
当 $(x+a)^n\equiv(x^n+a)(\text{mod}\ n)$ 时,n 为素数。
后续 ASK 被不同科学家多次改进,因此有多个版本,统称为 AKS 类算法。AKS 类算法也是目前效率最高的确定性算法,只要算法给出 true 的结果就一定是素数。
※ ChatGPT 与 Copilot 对本文亦有贡献。